![[cml_media_alt id='219']Dieci piccioni in nove caselle[/cml_media_alt]](https://insight.stefanopaladini.net/wp-content/uploads/2012/10/TooManyPigeons-300x243.jpg) The curious title of this page is the name of an important mathematical principle that is the argument of the following article.
The curious title of this page is the name of an important mathematical principle that is the argument of the following article.
The Pigeonhole Principle is a mathematical principle that is also known as “drawer principle”, “principio dei cassetti” in Italy and similarly “prince des tiroirs” in France, according to the name used for the first time by the mathematician who explained it, Peter Gustav Lejeune Dirichlet, in 1834 under the name of Schubfachprinzip (litterally “principle of the drawer”). But the english name “pigeonhole principle” is much more fun, also associated with the image you see on this page, taken from Wikipedia.
What is fascinating in this mathematical principle is the fact that, while it is extremely trivial and intuitive, in its basic formulation, its application can be quite difficult in particular cases and lead to surprising, unexpected and often counterintuitive results.
Referring to the image at the top of the article, an immediate statement could be: given a pigeonhole with 9 boxes and 10 pigeons, there will be for sure a cell that contains at least 2 pigeons.
So far… very trivial.
The trivial formulation of this principle is so intuitive that you can use it to create fun puzzles like this.
Six beds for seven travelers
A group of 7 travelers comes to a hotel, and demand a bed for every traveler.
The host replies, “I have only six beds distinguished by the letters A, B, C, D, E, F. But
I will try to adjust you all.”
So destined:
two travelers to sleep in the bed A,
then one in the bed B, and makes three,
then one in the bed C, and has four,
then one in the bed D, and has five,
then one in the bed E, and has six,
then take one of those who were in A and leads him in F, and has seven.
So the 7 travelers are sleeping in 6 beds, each in one bed.
How did he do?
In this example, our intuition screams that it’s not really possible that 7 people could find a place in 6 beds, each alone in one bed. The pigeonhole principle manifests itself automatically and prompts us to look for the trick in the formulation of the riddle.
In fact, it needs just a little of attention to realize that the seventh unfortunate traveler is left alone in the hotel lobby while one of his friends in the room A was counted twice.
A less immediate use of the same principle goes back to 1624, when Van Etten (pseudonym of Jean Leucheron) aims to demonstrate that in a city of 150,000 inhabitants there are two people that have the same number of hairs.
It is estimated that the hairy surface of a human head is 775cm2, and that each cm2 contains at most 165 hairs, with an average of 150.
So the maximum number of hair that may have a person is about 775 * 165 = 123 875 < 150 000. In a city with over a million inhabitants, like Rome, the probability that two people have the same number of hair is almost a certainty.
Formally, the principle states that if A and B are two finite sets and B has cardinality strictly less than A , then does not exists an from A to B.
A generalized version of the principle states that if there are n discrete objects that must be allocated in m containers, then there will be at least a container that will hold at least objects (the symbol
denotes the ceiling function).
Definitely more interesting is the probabilistic generalization of the principle. In this case we can say that if you put randomly n pigeons in pigeonhole of m cells, with uniform probability of 1/m, then at least one cell will contain more of one pigeon with probability:
where is a decreasing factorial. For n=0 and n=1 (with m>0), this probability is zero, while for n>m the probability is one, thus coinciding with the ordinary principle of the drawers.
As you can see, with a thorough analysis, a principle so intuitive leads to a far more complex formulation. In fact, there are cases in which the use of this intuitive principle fails miserably, (making us understand that the brain thinks in a logical manner only superficially), and a deeper analysis is needed.
Let’s look at a case in which the above rigorous formulation help us in solving a problem, known as the birthday paradox, formulated in 1939 by Richard von Mises .
The birthday paradox
Suppose that, during a party with thirty participants, a friend propose you to bet that at least two of the participants have the birthday on the same day.
Our intuition leads us to immediately apply the pigeonhole principle: to be sure that at least two people have birthday on the same day, it is necessary to have at least 367 guests (taking into account leap years). At this point the brain abandons logic to adopt an analog criteria: as the number of diners, we said about thirty, is very far from 367, which corresponds to a probability of 100%, then the probability that the event will occur is very scarce.
So you should bet for the contrary… or not? Let’s try to do a rigorous calculation.
To carry out the calculation, let’s use the formula for the probability of independent events: to make it easier, let’s assumes that the years are all of 365 days and that the birthdays are equally likely, even if that’s not accurate. Adding the leap day worsen slightly the chance, but on the other hand, the fact that birthdays are not equally likely raise it.
Let’s calculate first the probability that no date coincide, that is, let’s calculate the probability that all the dates are different. Take the first guest and get his date of birth, then let’s take a second. The probability that he has a date of birth different from the first guest is 364/365. Take a third guest. The likelihood that his birthday does not coincide with neither of the two already considered is 363/365 … and so on, until, for example, the fortieth guest, whose probability of being born on a different day from the previous 39 is 326/365. Being independent events, these numbers are multiplied together to obtain the probability that no birth date coincides.
If, in general, the number of guests is p then the probability that all p are born on different days is:
Thus, the probability that at least two guests were born on the same day is its complement:
Not so trivial now, isn’t it?
If we try to make the numerical calculation of this function and represent graphically the result, we find the graph here beside. The value of the probability rises very quickly even with a fairly small number of guests.
Indeed, already with a party of only 24 people, we have 54% of chances to win!
Even in a group of 23 people the probability is about 0.51, with 30 people it exceeds 0.70, with 50 people it touches even the 0.97, although to reach the certain event it is necessary to consider a group of at least 367 people.
And therefore is convenient to make a bet in favor: the probability of winning is very high!
 Una funzione si dice iniettiva se elementi distinti del dominio hanno un'immagine distinta, o equivalentemente se ogni elemento del codominio corrisponde al più ad un elemento del dominio.
Una funzione si dice iniettiva se elementi distinti del dominio hanno un'immagine distinta, o equivalentemente se ogni elemento del codominio corrisponde al più ad un elemento del dominio.Formalmente:
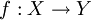 è iniettiva se
è iniettiva se 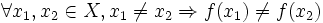
o equivalentemente: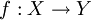 è iniettiva se
è iniettiva se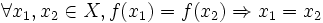
 -0
-0  )
)
Leave a Reply