Heart and chaos

A topological approach: Arthur Winfree

Mines’s work had highlighted the importance of speed and synchronization that stimuli across the heart should have for the organ to function optimally.
His approach, however, was still extremely tied to the medical-biological application and the description and interpretation of the results was purely physiological.
It was necessary for the genius of another character to make the pindaric jump that would allow the purely biological phenomenon to be linked to an underlying mathematical model much more abstract.

Here is depicted Arthur T. Winfree, a character whose multifaceted intelligence has led him to deal with a variety of topics mainly in the biological field, but applying theories and theories of mathematics, geometry and topology.
For this reason, he was defined a “theoretical biologist” and received the recognition of “genius” in 1984 from the MacArthur Foundation’s, the Norbert Wiener award in mathematics applied in 2000 and, most importantly, the Einthoven Award in 1989 for his work on the causes of ventricular fibrillation.
Much of Winfree’s work arises from his interest in the spontaneous synchronization phenomena of organic oscillators. Some examples: the thousands of sinus cell nodes producing a single collective electrical signal, the synchronization of male flashes of some firefly species that aggregate together on a single tree, or the thousands of mold cells that secrete synchronized pulses of AMP cyclical (a molecular signal that leads them to abandon lonely existence to start acting as a community body).
A first example of Winfree’s vision of periodic phenomena in biology is found in his doctoral thesis for Princeton University.
He studied the rhythms of sleep and wake of fruit flies in a time when everyone believed that this kind of circadian cycles were extremely robust, proving that relatively modest disruption could be enough to completely cancel them.
It is well known that the circadian cycle of sleep and wake persists even in dark or constant light conditions. This rhythm can be advanced by phase or delay by applying short light pulses. Winfree charted the “new phase” after the light pulse, depending on the “old phase” before the pulse, as the intensity and/or duration of the light changed.
He discovered that the behavior of flies fell into two characteristic schemes, shown in the figure below.

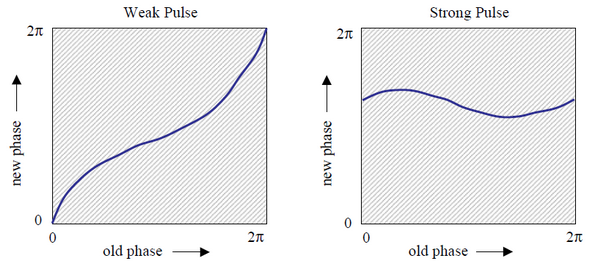
A weak impulse only causes a slight change in the phase, so the line of the new phase oscillates around the diagonal of the graph where “new phase” = “old phase”.
For strong disturbances, the oscillator resets to an almost constant phase value, regardless of the phase at the moment of the impulse. Then the chart shows a swing around a horizontal line where “new phase” = “constant”.
Winfree’s topological intuition consists of representing the two graphs on the surface of a thorus, since both axes are actually periodic dimensions in which the points at 0 and 2π have the same phase value. Let’s look at the image under this new representation.

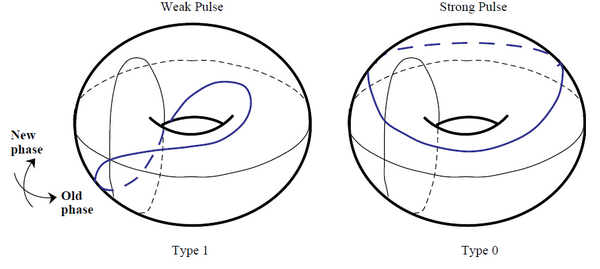
There is now a clear difference between the two behaviors: in the case of minor disturbances, the graph representing the new phase in function of the old passes one time through the center of the thorus (so it is of “type 1”) while in the case of the strong disruption the chart never passes through the center (so it is “type 0”).
The two graphs belong to two different topological invariants, so if there was a F function that binds the new phase with the old and the intensity of the stimulus, it can never be a continuous function because in this case it could not produce the jump, discontinuous, from type 1 to type 0.
Winfree therefore deduces that there must be a combination of phase and intensity of the stimulus for which the function F is indefinite and can experimentally demonstrate that such a point exists and de-synchronizes completely the sleep-wake cycle of a population of fl studied.

Subsequently Winfree’s interest moves on the spatial and temporal behavior of a category of chemical reactions called the Belousov-Zhabotinsky reactions. It is a family of highly oxidized redox reactions because, as reaction products have different colors, it is very interesting to see the kinetics of the reaction directly from observation of the formation of the compounds.

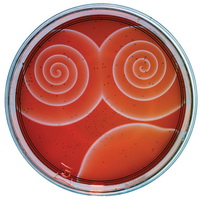If the reaction takes place in a very thin film of reagents, what comes out is a spiral formation as seen in the photo on the left.
spirale_lambda Once again Winfree makes a crucial remark on system topology.
In the image next to it is a rotating spiral. You can locate a phase point 0 identified with the “+” symbol and the circuits indicated by “0” and “1”. Each point along the two circuits will show oscillations over time of its state variables, while the spiral rotates, and there will also be a variation in space, moving along the circuit.
It is clear that the situation detected by the two circuits is substantially different because circuit 1 will see a variation of properties throughout the perimeter while circuit 0 will see the variation only in an angular range. Let’s see it graphically.

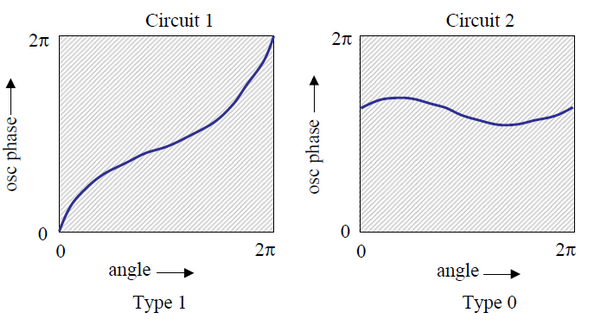
Does it remind you of something? Even then, Winfree notes that if there was a function to transform a generic λ lambda circuit from zone 1 to zone 0, it could not be continuous and there must be at least one point, indicated by “+”, where the phase is indefinite .

The next step is the three-dimensional extension of the phenomenon described above where the Phase Point 0 becomes a segment moving into space. The above-mentioned spiral then becomes a section of a more general three-dimensional scheme as shown in the image to the right. (Click on the image to see the animation).

Finally in 1983, Winfree published a research in which he illustrates a link between the spiral waves observations that are formed on the surface of the heart during fibrillation made by other scholars and his mathematical model.
He shows that an electrical stimulus of the right duration and right moment, which in the previous paragraph we have identified with the vulnerable period , can lead to the formation of spiral waves, causing tachycardia, which may, in appropriate conditions, fragment into a quantity of propagated waves in the tissue muscular and gives rise to fibrillation.

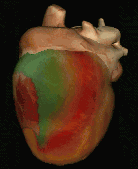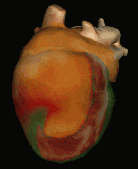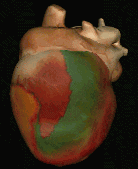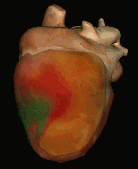Interesting 3D animations of these abnormal waves that can occur in the cardiac tissue are visible a this link:The Virtual HeartInteresting 3D animations of these abnormal waves that can occur in the cardiac tissue are visible a this link: The Virtual Heart