Hic sunt leones

La tradizione vuole che sulle mappe dell’antica Roma che rappresentavano le regioni africane, fosse indicata la locuzione Hic Sunt Leones (qui ci sono i leoni) per rappresentare le zone inesplorate, quindi possibilmente pericolose, su cui non v’erano dati certi.

In realtà non ci sono documenti storici che attestino questa convinzione in quanto le mappe in cui è possibile reperire questa indicazione, o una simile come hic sunt dracones, risalgono essenzialmente al medioevo. La mappa più antica in nostro possesso su cui sia leggibile un’iscrizione analoga, in questo caso “Hic abundant leones“, è la cosiddetta Cottoniana, risalente al 995 e rinvenuta nel 1598 da Sir Robert Cotton.
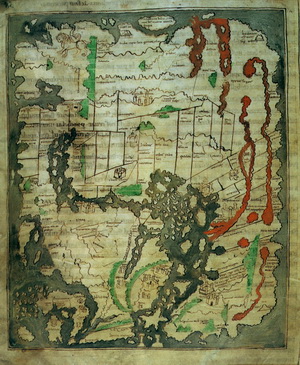La mappa, che potete vedere qui a fianco (cliccare per ingrandire), reca in alto l’iscrizione di cui ho riportato il dettaglio ed è organizzata, come molte mappe dell’epoca, con l’est verso l’alto. Quindi ad un lettore moderno appare ruotata di 90° in senso antiorario, con le colonne d’Ercole in basso e le isole britanniche a sinistra.
A parte l’orientamento inusuale dei punti cardinali sulla mappa, ciò che appare chiaro è che nel medioevo, la conoscenza della forma delle terre emerse, i profili delle coste, le distanze fra le varie località era, ad esser buoni, alquanto approssimativa.
Al giorno d’oggi tutte queste informazioni sono disponibili in grande quantità per cui il problema non è più il cosa scrivere su una mappa quanto il come scriverlo affinché la rappresentazione sia il più vicino possibile alla realtà.
Di questo problema, come vedremo più avanti, si occupa la cartografia.

La forma della Terra

La necessità di misurare ed elaborare le misurazioni relative agli appezzamenti di terreno ha una storia molto antica, infatti la culla della disciplina che oggi chiamiamo geometria (γεωμετρία, composto da geo che che deriva da γή, ghe = “terra” e μετρία, metria = “misura”) è sicuramente la civiltà egiziana. Oggi per individuare la disciplina che si occupa essenzialmente della misurazione del territorio si utilizza la parola geodesia (dal greco γῆ, ghe = “terra” e δαίω, daío = “divido”).
Dalla parola geodesia deriva anche la parola geodetica che viene usata per individuare le curve che localmente rappresentano la traiettoria più breve fra punti di un particolare spazio.
In matematica la definizione di spazio e di geodetica hanno carattere molto generale, ma ai fini della geodesia terrestre gli spazi che ci interessano sono essenzialmente due: il piano e la sfera, essendo il primo lo spazio di destinazione, su cui vogliamo fare la nostra rappresentazione e il secondo, con qualche precisazione, lo spazio di partenza dell’oggetto che vogliamo rappresentare.
La prima cosa da osservare è che le geodetiche hanno caratteristiche diverse a seconda dello spazio in cui sono definite.
Nell’esempio in figura vediamo cosa succede se proviamo a disegnare un triangolo sulla superficie di un cilindro congiungendo i vertici con delle linee geodetiche.

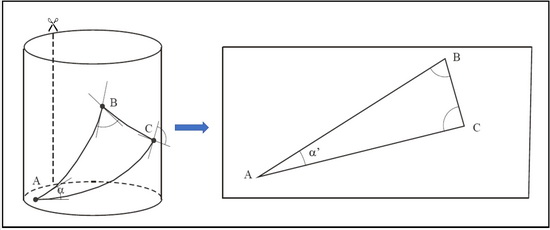
Come si può facilmente verificare in pratica con un foglio di carta e un paio di forbici, il cilindro può essere facilmente sviluppato su un piano semplicemente eseguendo un taglio lungo una delle generatrici e il triangolo geodetico risultante non avrà più i lati costituiti da circonferenze di raggio massimo, ma da segmenti di retta.
Tuttavia, se misuriamo la lunghezza dei lati e gli angoli che essi formano in corrispondenza dei vertici, scopriamo che né le lunghezze né gli angoli sono variati. Sia nel piano che sul cilindro la somma degli angoli interni del triangolo è sempre 180°.
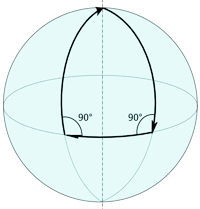Purtroppo questo non è più vero se consideriamo una sfera. In questo caso infatti le geodetiche si incontrano sempre in due punti ed è possibile costruire dei triangoli con due angoli retti, come visibile nell’esempio qui a fianco. Anzi, una delle caratteristiche peculiari della geometria sferica è proprio quella che la somma degli angoli interni di un triangolo è maggiore di 180°.
Appare chiaro che non c’è modo di trasferire una figura come questa su un piano senza pagare qualcosa in termini di deformazione di angoli e/o lunghezze e nei prossimi paragrafi vedremo come la cartografia abbia affrontato questo problema.

Prima di affrontare le proiezioni cartografiche è d’obbligo spendere ancora qualche parola sull’oggetto che vogliamo rappresentare, cioè la Terra.
La forma del nostro pianeta è tutt’altro che ideale.
Sappiamo che i corpi celesti, Terra compresa, sono modellati essenzialmente dalla forza di gravità. Sotto l’azione di questa forza, le particelle dotate di massa si muovono l’una verso l’altra nel tentativo di raggiungere una configurazione di minima energia. Le superfici equipotenziali, in un campo a simmetria centrale come quello gravitazionale sono delle sfere con centro nel centro di massa del sistema.
Quindi se la terra fosse costituita da particelle ideali, che non interagiscono fra di loro in nessun modo se non attraverso la forza di gravità, essa sarebbe una sfera perfetta.
Si dà il caso però che questa sfera perfetta sia anche in rotazione attorno al proprio asse per cui alla forza di gravità bisogna sommare un contributo dato dalla forza centrifuga che invece dipende dalla distanza dall’asse.
Si tratta quindi di un contributo radiale che sarà maggiore all’equatore e minore ai poli.
La somma di questi due contributi produce la forma di un ellissoide o, come si sente dire spesso, la Terra è una sfera “leggermente schiacciata ai poli“. Il raggio terrestre in corrispondenza dei poli risulta di circa 21km inferiore al raggio medio terrestre, pari a circa 6371km, quindi uno schiacciamento di appena lo 0.3%.
L’ultimo passo per definire la forma della terra consiste nel ricordarsi che essa non è composta da particelle ideali, ma da sostanze reali che si legano e interagiscono fra loro nei modi più vari. Sulla Terra vi sono materiali allo stato solido, liquido e, se vogliamo, anche gassoso e queste sostanze non possono muoversi indipendentemente le une dalle altre ma sono legate da forze di coesione di vario genere.
Il risultato è che la Terra è un ellissoide oblato e bitorzoluto per cui è stato necessario coniare un nome ad hoc: il geoide. Per definizione il geoide è una superficie perpendicolare in ogni punto alla direzione della verticale, cioè alla direzione della forza di gravità. La superficie del geoide è quindi definita dalla densità della superficie reale in ogni punto ed è oggi utilizzata come riferimento per la definizione delle quote altimetriche preferendola alla superficie dell’ellissoide medio.

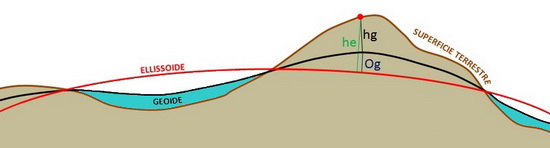
Infatti, mentre l’ellissoide è un’entità matematica definita in maniera esclusivamente geometrica, il geoide ha una origine fisica. Se ci muoviamo da una quota geoidica più bassa ad una più alta, stiamo effettivamente facendo un lavoro contro la forza di gravità e quindi avremo sempre la sensazione di “salire”. Questo non è necessariamente sempre vero per le quote ellissoidiche.