A prova d’errore

Raffiche di errori

In questo paragrafo parliamo dell’opera di uno scienziato che per primo ha avuto un approccio totalmente innovativo allo studio degli errori e della loro propagazione.
Lo vediamo raffigurato nell’immagine a destra: Benoît Mandelbrot.
Il titolo stesso di questo paragrafo coincide con quello utilizzato da Mandelbrot per il quarto capitolo del suo libro “Gli oggetti frattali”.
L’ambito in cui si sviluppa questo studio dell’errore è quello delle linee di trasmissione dati e bisogna ritornare indietro fino alla fine degli anni ’50, periodo in cui Mandelbrot era impiegato presso l’IBM.
La trasmissione di dati digitali era allora agli albori, gli scienziati conoscevano già le modalità con cui una linea di trasmissione potesse captare dei rumori dall’ambiente e come il segnale si deteriorasse di conseguenza, ma il fenomeno che era chiamato a studiare Mandelbrot era qualcosa che sfidava tutte le tecniche usate fino ad allora per combattere gli errori di trasmissione.
Su una linea di trasmissione digitale, il segnale che viene trasmesso rappresenta degli zero e degli uno che costituiscono dei numeri binari. Per esempio un valore alto di tensione sul filo può rappresentare un uno e un valore basso uno zero, o viceversa.
Accade che il rumore distorca a tal punto il segnale da trasfomre un uno in uno zero o viceversa introduca un uno laddove avrebbe dovuto esserci uno zero.
La cosa interessante è che pur aumentando la potenza dei dispositivi di trasmissione, il fenomeno continuava a presentarsi!
Ciò che veniva osservato erano intervalli di diverse ore in cui non si rilevava nessun errore intervallati da momenti in cui gli errori erano particolarmente fitti.
All’interno di queste pause della durata di ore però gli errori erano a loro volta raggruppati in raffiche separate da intervalli di circa 6 minuti. E fra una raffica e l’altra ogni 6 minuti vi erano dei raggruppamenti separati da intervalli di 36 secondi e così via.
L’approccio di Mandelbrot al problema fu quello del matematico: egli cercò dapprima un modello teorico che rappresentasse il fenomeno e lo individuò in quella che era comunemente nota come Polvere di Cantor.

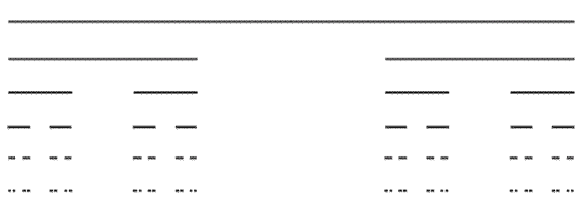
Quella che vediamo qui sopra rappresentata è un’immagine che illustra il metodo per costruire un insieme di punti detto appunto Polvere di Cantor.
Si tratta di un processo iterativo ripetuto all’infinito.
Si consideri un segmento di lunghezza unitaria. Da questo segmento se ne cancelli il terzo centrale in modo da avere due estremità lunghe 1/3 separate da uno spazio lungo anch’esso 1/3.
Si esegua lo stesso procedimento sui due segmenti rimanenti. Si otterranno 4 segmenti più piccoli lunghi 1/9… e così via all’infinito.
E’ importante notare che ogni volta che si cancella una parte di un segmento, le parti restanti contengono gli estremi.
Per questo motivo, una volta eseguite le infinite cancellazioni, ci ritroveremo con una polvere di punti la cui lunghezza totale è nulla, ma si tratta comunque di un insieme non vuoto, perchè conterrà sempre i punti estremi di ciascun segmento. Cioè i punti 0 e 1, 1/3 e 2/3, 1/9, 2/9, 7/9, 8/9, ecc.
Per costruire l’intero assieme, dopo questa operazione di interpolazione, vi è una fase di estrapolazione in cui la polvere ottenuta sul segmento 0-1 viene raddoppiata sul segmento 2-3.
Poi si ripete il processo raddoppiando l’intero assieme 0-3 sul segmento 6-9 e così via.
La sequenza di punti separati da intervalli più o meno grandi raggruppati fra loro in raffiche risulta essere molto molto vicina a ciò che viene osservato riguardo gli errori su una linea di trasmissione nella realtà.
Un’altra interessante proprietà di questo assieme, che forse è proprio quella che ha indotto Mandelbrot ad associarla con i suoi errori di trasmissione, è l’autosomiglianza. Infatti ingrandendone una piccola porzione per un opportuno fattore si ottiene di nuovo tutto l’assieme.
Naturalmente l’insieme di Cantor così definito è una costruzione matematica piuttosto astratta. Per calarla nel mondo reale e renderla adatta a descrivere il fenomeno fisico, Mandelbrot dovette rimaneggiarla un bel po’. Nel fenomeno reale infatti non abbiamo una origine di riferimento a partire dalla quale possiamo posizionare il nostro segmento da suddividere, nè sappiamo in quale punto del segmento ci si trovi in un dato istante di tempo. Per non contare il fatto che nella realtà non possiamo dividere alcunché un numero infinito di volte!
Nel segnale fisico vi è un valore minimo di durata di ciascun simbolo, per esempio un 1 è un segnale che ha una durata minima per cui non ha senso considerare una polvere di Cantor in cui la suddivisione ha raggiunto valori più piccoli della durata del simbolo elementare.
Mandelbrot individua due valori di scala, che chiama η e Λ, per individuare gli estremi minimo e massimo di suddivisione e estrapolazione e ad una sequenza così limitata applica dei procedimenti di randomizzazione tali che non vi siano zone statisticamente privilegiate al suo interno. Egli ha poi ulteriormente raffinato il suo modello fino ad ottenere un modello statistico che meglio descrivesse le sue raffiche di errori, ma ciò che si vuole sottolinerare in questo paragrafo è che, anche in questo caso, a nulla vale il miglioramento della qualità delle linee e la potenza dei dispositivi coinvolti nello scambio dei dati!
Gli errori ci sono sempre e si comportano in maniera alquanto subdola.
Nei prossimi paragrafi esaminiamo alcuni modi concreti per gestirli e conviverci.