A prova d’errore

Non sono solo canzonette

Il 17 agosto 1982 il primo CD per utilizzo commerciale venne prodotto in una fabbrica della Philips ad Hannover in Germania: La Sinfonia delle Alpi di Richard Strauss diretta da Herbert Von Karajan con la Berliner Philharmoniker. La foto di un iridescente dischetto da 12cm sarebbe stata sicuramente più rappresentativa dell’argomento di questo paragrafo, ma ho preferito aprire con un’immagine più gradevole come il ritratto del celebre compositore.

Il Compact Disc ha ormai compiuto 40 anni e la sua paternità spetta ad una joint venture tra DuPont e Philips che, verso la metà degli anni 70, gettarono le basi per realizzare un dispositivo robusto e versatile per l’archiviazione della musica ad alta qualità. La DuPont, che aveva partecipato inizialmente per cercare un nuovo impiego commerciale per il policarbonato di cui deteneva il brevetto, si tirò indietro dopo i primi studi preliminari. I nuovi dispositivi per la lettura dei compact disc sembravano troppo costosi per avere una grossa diffusione sul mercato e gli stessi dischi, con una capacità stimata di 600MB, sembravano troppo avanti rispetto alle capacità di archiviazione dei supporti in uso all’epoca. Ricordiamo che in quel periodo una dimensione tipica per un hard disk da computer era intorno ai 20MB.
Il progetto fu poi portato avanti da una joint venture fra Philips e Sony, che firmarono anche la stesura del cosiddetto Red Book (1982). Cioè il documento che definisce nei dettagli il modo con cui vengono codificati i dati da registrare sul supporto ottico.

Mentre nell’ascolto di un tradizionale disco in vinile è il nostro orecchio a filtrare i crepitii e i fruscii dovuti alla polvere che si deposita sui microsolchi, nei compact disc è necessario mettere il microprocessore nelle condizioni di interpretare correttamente le informazioni presenti sul disco. Graffi, sporcizia, impronte e in generale il deterioramento della superficie del supporto, da un punto di vista del processore, non sono altro che errori di lettura.
Nella definizione dello standard di codifica è stato necessario quindi inserire dei sistemi di correzione dell’errore e, come vedremo, i padri del CD non si sono fatti mancare nulla!

Innanzitutto cerchiamo di quantificare il messaggio originale che si vuole memorizzare.
La musica che deve essere memorizzata sul supporto digitale deve essere dapprima digitalizzata. Nel caso del CD si usa una frequenza di campionamento di 44100Hz e la dimensione dei campioni è di 16 bit.
La sorgente si considera sempre stereo quindi il flusso di informazione totale è di 44100 x 16 x 2 = 1411200 bit al secondo, cioè circa 172KB/s.

Ciò che viene memorizzato però non è il flusso continuo di suono digitalizzato, ma piuttosto una sequenza di “pacchetti” detti frames che contengono solo 6 campioni di musica per ciascun canale. In totale 6 campioni da 16 bit per canale, cioè 24 bytes.
A questi 24 bit di informazione “utile” si aggiunge una certa quantità di ridondanza avente principalmente la funzione di individuazione e correzione degli errori.

Controllo di Parità

Il primo meccanismo che viene impiegato per il controllo degli errori sui CD è il cosiddetto controllo di parità.
Si tratta di uno dei meccanismi più semplici e consiste nel contare il numero di 1 presenti nel messaggio che si vuole trasmettere e aggiungere un 1 o uno 0 al messaggio finale per fare in modo che esso abbia sempre la stessa parità.
Per esempio se il messaggio è M=100101 esso avrà parità dispari contenendo tre 1. Si può quindi scegliere di creare un messaggio T con parità pari aggiungendo un 1: T=1001011, oppure un messaggio con parità dispari aggiungendo uno 0: T=1001010.
In questo modo il ricevitore può eseguire il controllo di parità sul messaggio T ricevuto e aspettarsi di trovare sempre un valore di parità pari o dispari a seconda dello standard adottato. In presenza di un risultato diverso avrebbe la certezza di essere in presenza di un errore, o di un numero dispari di errori. La vulnerabilità di questo sistema è ovviamente che è insensibile ad un numero pari di errori. Anche un sistema così semplice può essere però utilizzato in modo da permettere una certa capacità di correzione se lo si applica a blocchi in modo da conferirgli una certa ciclicità.
Nell’immagine seguente vediamo un esempio di un blocco di messaggio, a sinistra, rappresentato come una matrice. Quelli visibili sotto e a destra delle linee blu sono i bit calcolati rispettivamente per ciascuna colonna e ciascuna riga. Nella parte destra dell’immagine vediamo lo stesso messaggio in cui un bit, a causa di un errore, è stato trasformato da 1 a 0. Confrontando il bit di parità calcolato sia per le righe che per le colonne si può individuare in quale incrocio si trova l’errore.

Per rendere più efficace il meccanismo del controllo di parità, nei CD esso viene utilizzato in congiunzione con un’altra tecnica: l’interlacciamento.

La codifica CIRC

L’acronimo CIRC sta per Cross-Interleaved Reed-Solomon Code e rappresenta una tecnica per “mescolare” fra loro i bit del messaggio da codificare in modo che eventuali raffiche di errori non lo danneggino in modo irrecuperabile.
Per illustrare meglio il funzionamento della tecnica di interlacciamento è meglio affidarsi ad un esempio.

Supponiamo che il messaggio da trasmettere sia:

Un danneggiamento del supporto potrebbe portare al cancellamento di una parte significativa del messaggio, per esempio:

Sorvoliamo sull’evidente riconoscibilità del verso del Leopardi usato nell’esempio e notiamo che in questo caso la particella “mi” in esso contenuta è completamente scomparsa a causa dell’errore.
Se invece sottoponiamo il messagio ad un processo di interlacciamento troviamo qualcosa del tipo:

Se il messaggio interlacciato avesse lo stesso danneggiamento visto sopra diventerebbe:

Ma l’applicazione all’inverso di un processo di deinterlacciamento porta ad un messaggio originale come segue:

Che è molto più “riconoscibile” in quanto nessuna parola è stata distrutta completamente.

Tornando alla costruzione del frame di dati per un cd, ai 24 byte del materiale musicale di partenza vengono quindi aggiunti 4 byte di parità e, dopo aver effettuato il processo di interlacciamento se ne aggiungono altri 4 per un totale di 32 byte.
Oltre i 32 byte di parità si aggiunge ora un singolo byte detto di subcode il quale contiene delle informazioni sulla traccia e sulla sincronizzazione. Questo byte è funzionale per il lettore CD e non è, in sè, un’aggiunta necessaria per il controllo dell’errore.

Vediamo adesso l’ultima codifica che viene fatta sui dati prima di essere registrati sul supporto ottico.

Codifica EFM

La sigla EFM sta per Eight to Fourteen Modulation. Per capire meglio la necessità di questo ulteriore passaggio di codifica del segnale, può essere utile vedere come appare la superficie di un CD osservata al microscopio.

Quello che appare un disegno a tratto-punto, come se fosse un codice Morse, è effettivamente la superficie del CD su cui sono presenti dei “rilievi”. La testina laser che effettua la lettura rileva la variazione di intensità della luce riflessa da questi rilievi e la converte in segnale digitale.
Ciò che è interessante è che la testina non associa uno 0 ad una “valle” e un 1 ad una “cresta”, come sarebbe intuitivo pensare, ma associa un 1 ad ogni variazione di intensità. Quindi l’uno sarà il risultato del passaggio del laser da una cresta ad una valle o viceversa.

Appare evidente che, se nel messaggio ci fossero due 1 vicini, questi non sarebbero praticamente rilevabili e inoltre, per rendere ancora più robusta la codifica nei confronti di errori, dovuti anche dalle eventuali variazioni di velocità del disco, è importante che gli 1 siano quando più sparpagliati possibile all’interno della parola di codice.

Per questo motivo è stata costruita una che associa ad ogni codice numerico di 8 bit un univoco codice su 14 bit fatto in modo che fra due 1 successivi vi siano sempre almeno due 0 e al massimo 10. In questo modo si riesce rendere distinguibili gli 1, avere una buona densità di informazione e permettere alla testina laser di essere sempre a fuoco sul supporto.
Nell’immagine seguente vediamo illustrato l’intero processo di lettura.

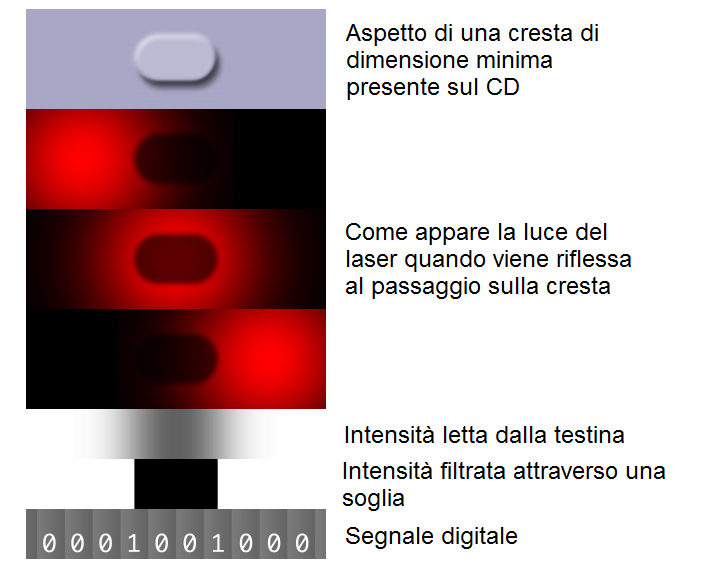
Quindi per ogni byte di informazione che vogliamo inserire nel nostro frame dobbiamo utilizzare una corrispondente parola di 14 bit scelta nella tabella EFM con l’aggiunta di 3 ulteriori bit, detti merge bit, che servono a fare in modo che la condizione di due zeri minimo e 10 zeri massimo sia conservata anche fra due parole adiacenti e non solo all’interno della stessa parola. In totale abbiamo 17 bit per ogni 8 bit di informazione da codificare.

Infine all’inizio di ogni frame si aggiungono ulteriori 24 bit più 3 merge bit che rappresentano un codice di sincronizzazione.

In totale abbiamo raggiunto ben 588 bit di informazione per riuscire a trasmentterne 192. Cioè solo il 33% di quanto viene registrato su un CD è reale segnale musicale. I due terzi sono informazioni necessarie a rendere il sistema robusto nei confronti dell’errore!