Cuore e caos

Un approccio topologico: Arthur Winfree

Il lavoro di Mines aveva messo in luce l’importanza della velocità e della sincronizzazione che gli stimoli che attraversano il cuore devono avere affinchè l’organo funzioni in maniera ottimale.
Il suo approccio rimaneva comunque estremamente legato alla applicazione medico-biologica e la descrizione e interpretazione dei risultati si svolgeva puramente nell’ambito fisiologico.
Era necessario il genio di una altro personaggio, per fare il salto pindarico che permettesse di collegare il fenomeno puramente biologico con un sottostante modello matematico molto più astratto.

Nella fotografia a fianco è raffigurato Arthur T. Winfree, un personaggio la cui poliedrica intelligenza l’ha portato ad occuparsi di svariati argomenti prevalentemente in ambito biologico, ma applicandovi metodi e teorie propri della matematica, della geometria e della topologia.
Per questo motivo è stato definito un biologo teorico ricevendo il riconoscimento di “genius” da parte delle MacArthur Foundation nel 1984, il premio Norbert Wiener in matematica applicata nel 2000 e, quello che più ci interessa in questa sede, il premio Einthoven nel 1989 per il suo lavoro sulle cause della fibrillazione ventricolare.
Gran parte del lavoro di Winfree nasce dal suo interesse per i fenomeni di sincronizzazione spontanea di oscillatori biologici. Alcuni esempi: le migliaia di cellule del nodo senoatriale che producono un unico segnale elettrico collettivo, la sincronizzazione dei flash dei maschi di alcune specie di lucciole che si aggregano insieme su un unico albero oppure le migliaia di cellule di muffa che secernono impulsi sincronizzati di AMP ciclico (un segnale molecolare che le guida ad abbandonare l’esistenza solitaria per iniziare a comportarsi come un organismo comunitario).
Un primo esempio della visione di Winfree dei fenomeni periodici in biologia lo troviamo nella sua tesi di dottorato per le Princeton University.
Egli studiò i ritmi di sonno e veglia dei moscerini della frutta in un epoca in cui tutti credevano che questo tipo di cicli circadiani fossero estremamente robusti, dimostrando che può essere sufficiente una perturbazione relativamente modesta per annullarli completamente.
E’ noto che il ciclo circadiano di sonno e veglia persista anche in condizioni di buio costante o scarsa illuminazione. Tale ritmo può essere avanzato di fase o ritardato tramite l’applicazione di brevi impulsi di luce. Winfree diagrammò la “nuova fase”, dopo l’impulso luminoso, in funzione della “vecchia fase”, prima dell’impulso, al variare dell’intensità e/o durata dello stesso.
Scoprì che il comportamento dei moscerini ricadeva in due schemi caratteristici, mostrati nella figura sotto.

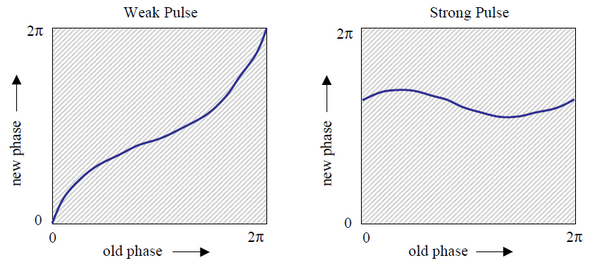
Un impulso debole causa solo una leggera variazione nella fase, quindi la linea della nuova fase oscilla intorno alla diagonale del grafico dove “nuova fase”=”vecchia fase”.
Per forti perturbazioni, l’oscillatore si resetta su un valore di fase quasi costante, indipendentemente dalla fase presente al momento dell’impulso. Quindi il grafico mostra un’oscillazione attorno ad una linea orizzontale dove “nuova fase”=”costante”.
L’intuizione topologica di Winfree consiste nel rappresentare i due grafici sulla superficie di un toro, dal momento che entrambi gli assi sono in realtà delle grandezze periodiche in cui i punti a 0 e 2π hanno lo stesso valore di fase. Vediamo nell’immagine sotto questa nuova rappresentazione.

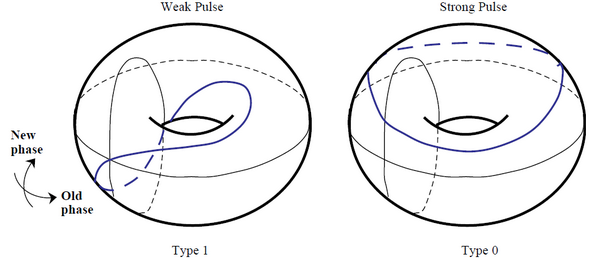
Appare chiara adesso una sostanziale differenza fra i due comportamenti: nel caso delle piccole perturbazioni, il grafico che rappresenta la nuova fase in funzione della vecchia passa una volta attraverso il centro del toro (quindi è di “tipo 1”) mentre nel caso delle forti perturbazioni il grafico non passa mai attraverso il centro (quindi è di “tipo 0”).
I due grafici appartengono a due invarianti topologici diversi, quindi se esistesse una funzione F che lega la nuova fase con la vecchia e con l’intensità dello stimolo, essa non potrà mai essere una funzione continua perchè in questo caso non potrebbe produrre il salto, discontinuo, dal tipo 1 al tipo 0.
Winfree deduce quindi che deve esistere una combinazione di fase e intensità dello stimolo per cui la funzione F è indefinita e riesce sperimentalmente a dimostrare che tale punto esite, desincronizzando completamente il ciclo sonno-veglia di una popolazione di moscerini oggetto di studio.

Successivamente l’interesse di Winfree si sposta sul comportamento spaziale e temporale di una categoria di reazioni chimiche denominate reazioni di Belousov-Zhabotinsky. Si tratta di una famiglia di reazioni di ossidoriduzione molto studiate perchè, siccome i prodotti di reazione hanno colori diversi, è molto interessante vedere la cinetica della reazione direttamente dall’osservazione della formazione dei composti.

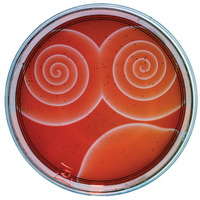Se si fa avvenire la reazione in un film molto sottile di reagenti, quello che ne viene fuori è una formazione a spirale come visibile nella foto a sinistra.
Ancora una volta Winfree fa un’osservazione cruciale sulla topologia del sistema.
Nell’immagine a fianco è rappresentata una spirale rotante. Si può individuare un punto a fase 0 identificato con il simbolo “+” e dei circuiti indicati con “0” e “1”. Ciascun punto lungo i due circuiti presenterà delle oscillazioni nel tempo delle sue variabili di stato, mentre la spirale ruota, e inoltre vi sarà una variazione nello spazio, muovendosi lungo il circuito.
Appare chiaro che la situazione rilevata dai due circuiti è sostanzialmente diversa perchè il circuito 1 vedrà una variazione delle proprietà lungo tutto il perimetro mentre il circuito 0 vedrà la variazione solo in un intervallo angolare. Vediamolo graficamente.

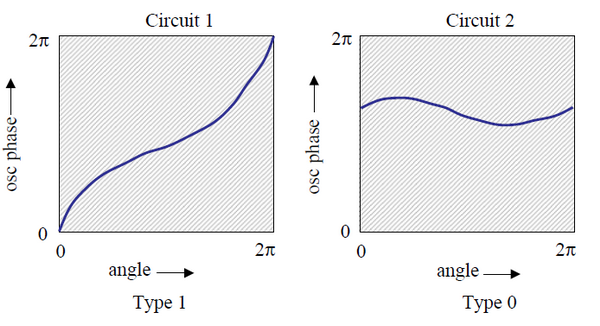
Ricorda qualcosa?　Anche in questo caso Winfree nota che se esistesse una funzione per trasformare un generico circuito λ lambda dalla zona 1 alla zona 0, essa non potrebbe essere continua e deve esistere almeno un punto, quello indicato con “+”, in cui la fase risulti indefinita.

Il passo successivo è l’estensione tridimensionale del fenomeno sopra descritto in cui il punto a fase 0 diventa un segmento che si sposta nello spazio. La spirale sopra rappresentata diventa quindi una sezione di uno schema tridimensionale più generale come mostrato nell’immagine a destra. (Cliccare sull’immagine per vedere l’animazione).

Finalmente nel 1983 Winfree pubblica una ricerca in cui illustra un collegamento fra le osservazioni di onde a spirale che si formano sulla superficie del cuore durante la fibrillazione fatte da altri studiosi e il suo modello matematico.
Egli dimostra che uno stimolo elettrico della giusta durata e nel giusto momento, che nel paragrafo precedente abbiamo identificato col periodo vulnerabile, può portare alla formazione di onde a spirale, causanti tachicardia, che in opportune condizioni possono frammentarsi in una quantità di onde propagantisi nel tessuto muscolare e dando luogo a fibrillazione.

Interessanti animazioni 3D di queste onde anomale che possono instaurarsi nel tessuto cardiaco sono visibili a questo link: The Virtual Heart