L’inafferrabilità del caos

Noto semplicemente come Principia, il “Philosophiae Naturalis Principia Mathematica” è un trattato in tre libri di Isaac Newton, pubblicato il 5 luglio 1687.
La pubblicazione di questo libro è considerata, a ragione, una pietra miliare nella storia della scienza. Nei Principia, Newton fornisce le tre leggi della dinamica e la legge della gravitazione universale:

\displaystyle F{_{g}}=G\frac{m_{1}m_{2}}{r^{2}}

utilizzando il formalismo matematico che oggi ci è familiare, ma non solo. Nei Principia è contenuta anche una descrizione sintetica di quello che egli chiama il Metodo delle Flussioni e che oggi si è evoluto nel moderno Calcolo Infinitesimale.
Newton aveva fornito alla comunità scientifica, non solo degli strumenti potentissimi per studiare l’universo, ma aveva anche mostrato come usarli. E gli scienziati li usarono!

Gli anni successivi furono densi di scoperte in campo matematico e fisico. Il calcolo infinitesimale e lo studio delle funzioni si arricchì presto di teoremi che ne amplificarono la potenza e la portata e la sua applicazione ai vari fenomeni portò alla comprensione e descrizione dei sistemi più disparati. Gli astronomi poterono predire con precisione i movimenti dei pianeti proiettando la loro analisi anni nel futuro.

L’onda di questi successi scientifici portò ad una sorta di euforia da determinismo che può essere ben riassunta dalla celebre frase che Laplace inserì nell’introduzione al suo trattato sulla probabilità:

«Possiamo considerare lo stato attuale dell’universo come l’effetto del suo passato e la causa del suo futuro. Un intelletto che ad un determinato istante dovesse conoscere tutte le forze che mettono in moto la natura, e tutte le posizioni di tutti gli oggetti di cui la natura è composta, se questo intelletto fosse inoltre sufficientemente ampio da sottoporre questi dati ad analisi, esso racchiuderebbe in un’unica formula i movimenti dei corpi più grandi dell’universo e quelli degli atomi più piccoli; per un tale intelletto nulla sarebbe incerto ed il futuro proprio come il passato sarebbe evidente davanti ai suoi occhi»
(Essai philosophique sur les probabilités, Laplace)

La situazione descritta da Laplace assomiglia pericolosamente a quella del paragrafo precedente! Vediamo se nel campo della fisica teorica le cose vanno meglio che in filosofia.

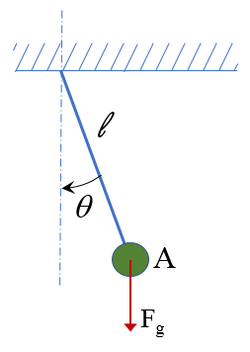Uno dei sistemi fisici ideali più studiati dagli studenti è il cosiddetto pendolo semplice.
Come vediamo in figura si tratta di un sistema costituito da una massa A vincolata tramite un filo di lunghezza l ad oscillare appesa ad un soffitto.
Alla descrizione di questo sistema si aggiungono alcune ipotesi semplificative, come considerare il filo inestensibile e di massa trascurabile e trascurare l’estensione spaziale della massa A che si dice quindi puntiforme.
In sostanza è come dire che vogliamo studiare il movimento di un punto che può solo ruotare attorno ad un centro posto a distanza fissa. Il fatto di chiamarlo “pendolo” serve solo ad aiutare l’immaginazione.
Il motore del sistema è la forza di gravità Fg che agisce sulla massa A, che quindi è orientata sempre verso il basso e la legge che regola l’interazione della forza con la massa è proprio la legge di Newton, F=ma.
In questo sistema semplificato, una parte della forza di gravità sarà contrastata dall’azione del filo quindi andremo a considerare solo la parte di forza di gravità che agisce in direzione della traiettoria circolare della massa.
E la posizione della massa stessa può essere determinata conoscendo esclusivamente il valore dell’angolo theta che il filo forma con la verticale.
Facendo le opportune semplificazioni la legge di Newton applicata al pendolo è la seguente:

\displaystyle \ddot{\theta}=-\frac{g}{l}sin \theta

cioè l’accelerazione angolare che subisce la massa dipende dal seno dell’angolo che il pendolo forma con la verticale.
Il che ha perfettamente senso in quanto possiamo facilmente immaginare che la forza di gravità si eserciti appieno quando il pendolo è a 90°, al massimo della sua oscillazione, e sia nulla quando il pendolo transita per la verticale, quando tutta la forza è controbilanciata dalla reazione del filo.
Bene. A questo punto la spiegazione prosegue supponendo che le oscillazioni del pendolo siano “piccole” in modo da poter confondere il valore del seno dell’angolo con l’angolo stesso.
Sotto questa ipotesi, l’equazione di cui sopra si semplifica notevolmente tanto da poter essere risolta:

\displaystyle \ddot{\theta}+\frac{g}{l}\theta=0\Rightarrow \theta \left ( t \right )=\theta _{0}cos\left ( \omega t + \phi \right )

con \displaystyle\omega =\sqrt{\frac{g}{l}} .

L’espressione \displaystyle \theta \left ( t \right )=\theta _{0}cos\left ( \omega t + \phi \right ) è detta oscillatore armonico e permette di prevedere la posizione della massa A in qualunque istante del tempo nel passato e nel futuro.
Il sogno di Laplace fatto realtà!
Peccato che questa soluzione ignori l’elefante nella stanza, cioè aver buttato dalla finestra la funzione seno.
Certo, qualcuno potrebbe pensare che, se avessimo considerato l’equazione nella sua forma originale (e fossimo stati in grado di risolverla) non avremmo trovato un risultato molto diverso. In fondo la massa, vincolata in quel modo, non può far altro che oscillare. Al massimo oscillerebbe in maniera leggermente diversa da quanto previsto dall’oscillatore armonico.

Purtroppo le cose non stanno sempre così! E basta complicare anche solo di poco l’esperimento ideale del pendolo semplice per trovarsi in una situazione completamente ingestibile.
Nella animazione che segue è possibile vedere il comportamento nel tempo di un Doppio Pendolo.

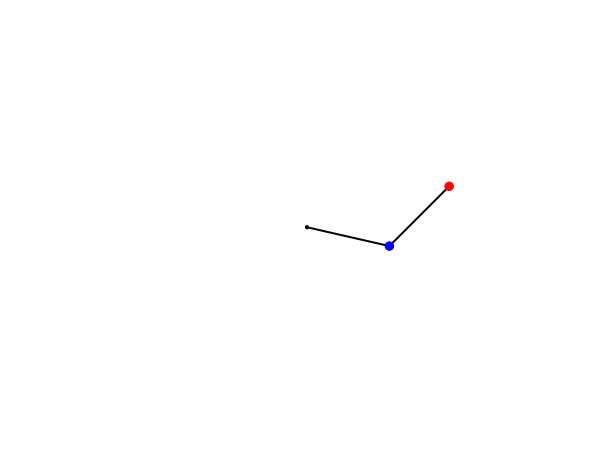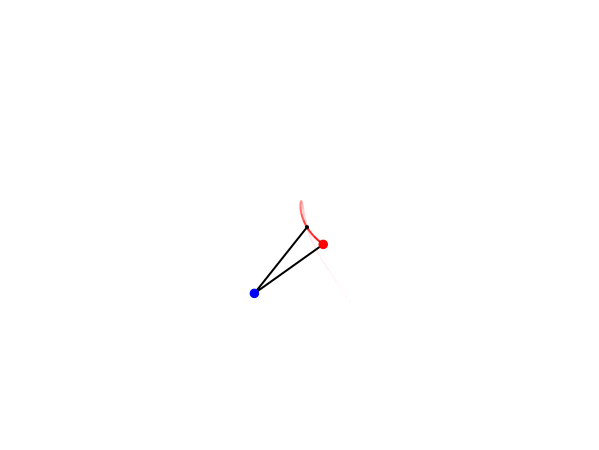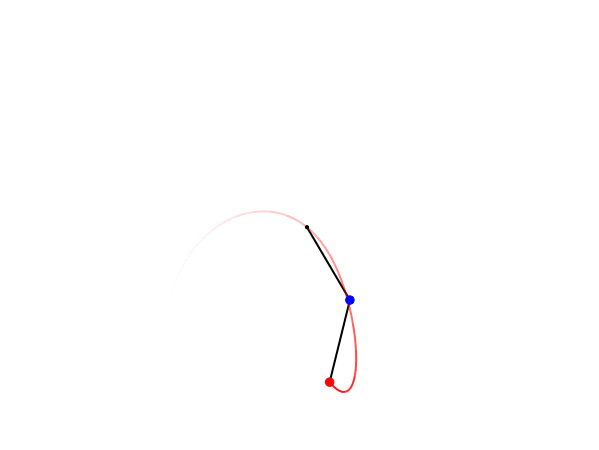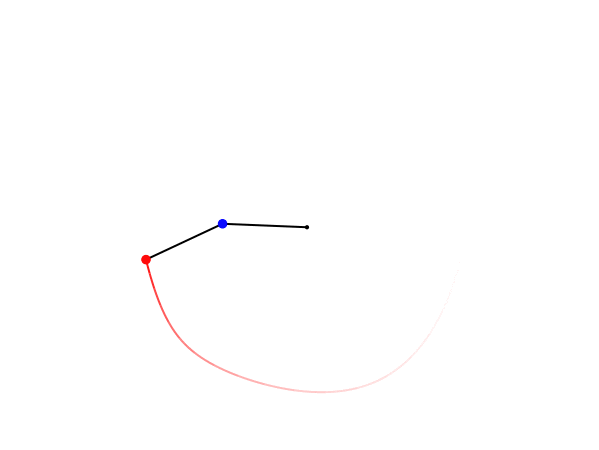
Come si può vedere, il movimento delle due masse è completamente caotico, non c’è semplificazione che tenga. Anche conoscendo perfettamente le leggi che governano il movimento delle due masse, che sono le stesse usate per il pendolo semplice, non c’è modo di conoscere quale sarà la loro posizione in ogni istante del tempo.
Ancora una volta abbiamo trovato un sistema che porta alla frustrazione delle nostra aspettative in termini di conoscenza.

Per completezza bisogna aggiungere che queste limitazioni, ancorché messe in secondo piano dagli sviluppi positivi delle teorie, erano be note allo stesso Newton il quale vi aveva fatto cenno anche nei Principia. In particolare possiamo citare il Problema dei tre corpi.
Si tratta dello studio del moto di tre corpi massicci sotto l’azione della forza di attrazione gravitazionale universale.
Se l’attrazione gravitazionale fra due corpi è descritta in maniera semplice ed elegante dalla formula che abbiamo riportato all’inizio del paragrafo, e se il moto di tali corpi può essere facilmente predetto da tale legge in un modo che avrebbe pienamente soddisfatto Laplace, l’entusiasmo svanisce se se ne vogliono considerare più di due.
Introdurre un terzo corpo nel sistema significa aggiungere le interazioni reciproche di tutte le combinazioni di un corpo con l’altro e la soluzione chiusa non è più possibile. Nell’animazione seguente vediamo una simulazione tratta da Wikipedia.

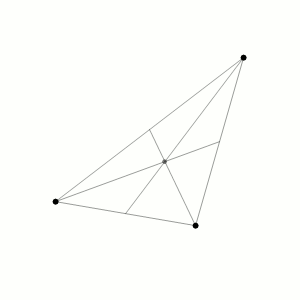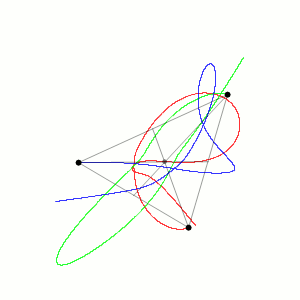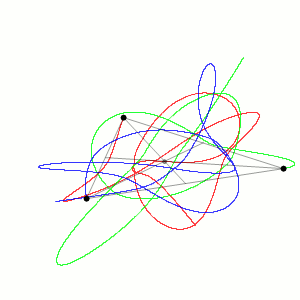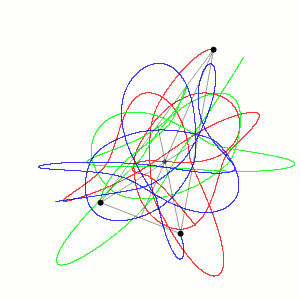
Dovremo aspettare l’era dei computer nel 1962 e l’opera di Edward Lorenz per gettare nuova luce sull’argomento, assistere alla nascita della teoria del caos e degli attrattori frattali. Ma questo è un argomento che meriterebbe un articolo a sé.

In pratica, nonostante la meravigliosa formula della gravitazione universale, il destino del Sistema Solare con tutti i suoi pianeti e corpi celesti assortiti, rimane un mistero incalcolabile…

←

Pagine: 1 2