Hic sunt leones

L’appiattimento della sfera

Lo scopo della cartografia è quello di trovare il modo di rappresentare la superficie, che abbiamo visto essere alquanto complessa, della Terra su un piano per poter essere facilmente visualizzata e stampata.
Nel paragrafo precedente abbiamo visto che il piano e la sfera, o nel nostro caso l’ellissoide, non vanno particolarmente d’accordo e non è possibile passare dall’una all’altro utilizzando un semplice sviluppo, ma è necessario ricorrere ad una proiezione, come vedremo più avanti.
L’esperienza comune però ci dice che la curvatura terrestre è qualcosa di estremamente difficile da percepire. La terra sembra piatta, l’orizzonte sembra piatto e ancora oggi c’è un discreto numero di persone convinte che lo sia veramente!
La verità è che il nostro pianeta è veramente enorme e, considerando un raggio medio di 6371km, anche su un aereo di linea che viaggia a 10000m dalla superficie, ci si è allontanati solo dello 0.2% da essa! Troppo poco perché la curvatura diventi veramente evidente.
E’ comunque lecito chiedersi a quanto ammonti l’errore, almeno localmente, nel considerare la superficie della terra piana anziché sferica. Questo torna utile anche per capire una eventuale proiezione di quanto si discosti dalla realtà.
Innanzitutto notiamo che la precisione con cui riusciamo ad effettuare dei rilievi sulla posizione degli oggetti sulla superficie reale della Terra è tale da autorizzarci a utilizzare l’ellissoide come superficie di riferimento al posto del geoide.
Considerazioni matematiche, che fanno uso degli sviluppi di Puiseux-Weingarten, ci autorizzano, per distanze fino a 100km, a considerare localmente la superficie di riferimento sferica anziché ellissoidica. L’errore che si compie nel riportare le distanze da un ellissoide ad una sfera nel raggio di 100km ammonta infatti a circa 28mm. Per le quote altimetriche la situazione è più restrittiva e bisogna restringere il raggio di equivalenza a circa 15-20km. Se rimaniamo nell’intorno dei 15-20km da un punto sulla superficie, allora è possibile confrontare una superficie sferica con una superficie piana ed utilizzare le semplici formule di trigoniometria per fare i calcoli. Il raggio di 15km in cui è possibile confondere l’ellissoide con una sfera è detto campo topografico.

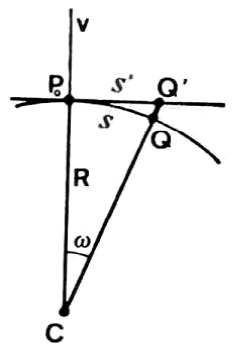Come passo ulteriore chiediamoci di quanto si sbaglia a sostituire un piano al posto di una sfera.
Con riferimento all’immagine a fianco, vogliamo stimare la differenza fra la distanza s misurata sulla sfera e la distanza s’ misurata sul piano.
Risulta che:

da cui, sviluppando la tangente e trascurando i termini di ordine superiore si ottiene:

che è l’errore relativo che si commette nel considerare s’ al posto di s.
Nel caso peggiorativo di R al suo valore massimo di 6378km e imponendo di contenere l’errore entro i 2mm, si trova che l’errore rimane così contenuto per un raggio di 15.6km.
Nel caso delle quote altimetriche il discorso è più delicato.
In questo caso l’errore da stimare è la distanza fra Q’ e Q:

Da cui sviluppando il radicale e trascurando gli ordini superiori si ottiene:

Su 10km l’errore ammonta già a 7.8m, quindi, se è richiesta una misura di precisione, non è lecito confondere la superficie sferica con il piano tangente.
Posto che, oltre i 15km di raggio, la nostra rappresentazione planare della Terra sarà soggetta ad un errore, andiamo ad analizzare i vari metodi che sono stati e sono tutt’ora utilizzati per la cartografia.