La relatività di Mercurio

Precessione e relatività

Proprio il movimento orbitale del pianeta Mercurio ci porta all’ultima parte di questo articolo in cui affrontiamo il tema della precessione del perielio della sua orbita.
Il volto ritratto in questa immagine è quello di Isaac Newton. Il suo contributo alla comprensione del moto dei pianeti è fondamentale e ancora oggi le sue formule sono perfettamente adatte a studiarne e calcolarne le orbite e a predirne i movimenti con grande precisione.
A parte qualche caso estremo come quello di Mercurio…
Agli inizi del 1600 l’astronomo tedesco Johannes von Kepler aveva formulato le sue famose tre leggi che descrivevano in maniera empirica e molto accurata le osservazioni fatte sul movimento dei pianeti. In particolare la prima legge asserisce che i pianeti percorrono delle orbite piane ellittiche di cui il Sole occupa uno dei fuochi e la seconda legge asserisce che il raggio vettore spazza aree uguali in tempi uguali, cioè i pianeti accelerano quando sono più vicini al sole e rallentano quando se ne allontanano.
Nel 1687 Newton, nel suo trattato Philosophiae Naturalis Principia Mathematica, propone una legge matematica per descrivere il modo in cui due corpi dotati di massa interagiscono fra di loro.
Da questa legge, nota come legge di gravitazione universale, si possono derivare le leggi di Keplero e di conseguenza essa diventa il fondamento per spiegare il moto dei pianeti nel sistema solare.
La formula è quella che tutti conosciamo, in cui si vede che la forza che le masse esercitano l’una sull’altra è proporzionale al prodotto delle due masse e inversamente proporzionale al quadrato della distanza che le separa.

Dato un campo di tipo centrale come quello espresso dalla legge di Newton, il fatto che le orbite siano ellittiche e le velocità dei pianeti varino come osservato, diventano delle conseguenze matematiche del tipo di campo.
Le leggi di Keplero sono valide sotto alcune ipotesi semplificative, in particolare la massa del pianeta deve essere trascurabile rispetto a quella del Sole e l’influenza dei vari pianeti l’uno sull’altro deve essere nulla.
Ovviamente Newton si rendeva conto di queste limitazioni e sapeva che il loro effetto faceva sì che l’intera orbita di un pianeta non fosse perfettamente costante ma ruotasse lentamente causando quella che viene chiamata precessione anomalistica.
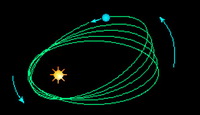Questo significa che, dopo una rivoluzione attorno alla stella, il pianeta non raggiungerà il perielio nello stesso punto da cui era partito, ma in un punto più avanti o più indietro in funzione del tipo di precessione. Per la Terra il tempo a compiere un giro completo, escludendo altri effetti di precessione, ammonta a 112000 anni.
Per Mercurio, essendo maggiore la sua velocità di rivoluzione, il fenomeno è più accentuato e si osserva una precessione di 5600 secondi d’arco al secolo. Newton calcolò, usando la sua formula, tutte le influenze dei vari pianeti sulle rispettive orbite e trovò dei valori di precessione che si accordavano alle osservazioni per tutti i pianeti tranne Mercurio. Secondo i suoi calcoli il valore sarebbe dovuto essere di 5557 secondi. Mancavano 43″ all’appello!
Una delle soluzioni proposte nel 1859 da Le Verrier, che forse sperava di ripetere il successo della scoperta di Nettuno, fu persino quella di ipotizzare l’esistenza di un ulteriore pianeta, più interno rispetto a Mercurio, denominato Vulcano.
Per avere la spiegazione, che oggi si considera definitiva, di questo fenomeno, bisognerà attendere il 1919 quando Einstein vi applicò la sua teoria della relatività generale.
Egli propose che, nello studio del moto di Mercurio, non fosse sufficiente considerare il campo gravitazionale generato dal Sole e il campo della forza centrifuga dovuto al movimento di rotazione, ma fosse necessario un terzo termine di origine relativistica, come visibile nell’equazione sotto riportata.

Sviluppando l’effetto di questo termine energetico aggiuntivo, per un’orbita ellittica, si scopre che essa è soggetta ad una precessione che può essere calcolata con la relazione seguente:

in cui compaiono il termine A che è il semiasse medio dell’orbita, e la sua eccentricità e ovviamente c la velocità della luce .

Il valore calcolato attraverso questa formula rende perfettamente conto di quanto osservato sperimentalmente ed è oggi considerato una delle prove più robuste della validità della teoria della relatività generale.