Non confondiamoci

Accuratezza-Precisone

Parlare di precisione e accuratezza ci costringe almeno un minimo ad entrare nel mondo della metrologia, che è la scienza che ha come oggetto di studio i problemi legati alla misurazione. Ma cosa intendiamo di preciso quando parliamo di precisione? In fondo, se siamo persone precise, vorremmo avere una definizione precisa cui fare riferimento per capire precisamente il significato e l’uso della parola “precisione“.
Come potete vedere l’uso comune di questa parola è alquanto versatile e infatti il vocabolario se la cava con un generico “rispetto dell’ordine e dell’esattezza“, pur di evitare di entrare nella miriade di sfumature che può assumere il suo significato in funzione del contesto in cui viene impiegata.In campo scientifico si parla necessariamente di precisione quando si ha a che fare con delle misurazioni e tipicamente viene affiancata al termine accuratezza perché è l’accoppiata di queste due coordinate che definisce la bontà di una misura.
In questo articolo avevamo affrontato il tema dell’errore e visto come, dato un insieme di misure essenzialmente inesatte, il calcolo della media ci possa dare un’indicazione su quale sia il valore vero di una grandezza.
In quella sede non avevamo fatto nessuna valutazione qualitativa sulle misure in sé, né su come esse fossero distribuite rispetto al valore cercato.
In realtà, quando si osserva l’entità e la distribuzione degli errori, si ricavano informazioni importanti sia sullo strumento di misura utilizzato, che, in parte, anche sul fenomeno stesso oggetto di studio.
Tipicamente per illustrare il significato dei termini precisione e accuratezza, si utilizza un grafico come quello seguente.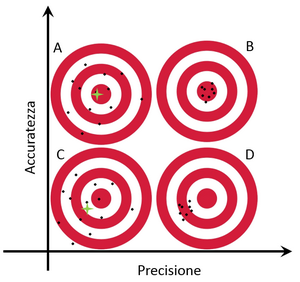Nel grafico vediamo illustrate quattro situazioni in cui differenti valori di precisione e accuratezza, crescenti nella direzione della freccia dei rispettivi assi, giocano un ruolo importante nel determinare la distribuzione delle misure effettuate, rispetto al valore vero rappresentato dal centro del bersaglio.
Il caso peggiore fra i quattro è sicuramente il caso C, in cui vediamo che i punti, che rappresentano le misure, sono sparpagliati attorno ad un valore medio indicato con una stella verde.
In questo caso le misure sono inconsistenti fra loro in quanto variano grandemente l’una dall’altra, e, mediamente, indicano un valore medio lontano dal valore vero. Si tratta di uno scenario in cui sia la precisione che l’accuratezza sono scarse.
Il caso A è quello in cui aumenta l’accuratezza. Le misure sono ancora sparpagliate, ma stavolta il valore medio è molto vicino al valore vero. E’ il tipico scenario in cui la misura è affetta da errori casuali, un rumore di fondo che fa sì che le misure differiscano molto fra loro ma, considerandole tutte insieme, l’effetto casuale tende a cancellarsi è il risultato finale risulta, appunto, accurato.
Il caso D è l’opposto del caso A. Qui vediamo l’effetto di un aumento della precisione nelle misure. I punti sono tutti molto vicini gli uni agli altri, segno di misure molto consistenti fra loro che si discostano poco dal valore medio individuato. Purtroppo in questo caso la scarsa accuratezza fa sì che questo valore sia comunque distante dal valore vero. E’ lo scenario tipico che deriva dalla presenza di errori sistematici, che si ripetono nello stesso modo in tutte le misure e che possono essere eliminati tramite una opportuna taratura degli strumenti.
Ovviamente il caso ottimale è quello contrassegnato dalla lettera B, in cui sia la precisione che l’accuratezza sono al massimo, segno che le misure sono state effettuate utilizzando strumenti di buona qualità in condizioni sperimentali ben controllate.
Riepilogando possiamo dire che le misure sono tanto più accurate quando più la media delle misure si avvicina al valore vero; le misure sono tanto più precise quanto più sono vicine alla loro media.
Un’ultima considerazione sui concetti di accuratezza e precisione riguarda l’entità dell’errore. Infatti la “vicinanza” e “lontananza” dal valore vero, di cui abbiamo scritto poco sopra, hanno senso solo in relazione all’entità del valore che si vuole misurare. Per misurare la distanza fra le pareti di una casa è necessaria una precisione del centimetro per essere sicuri che i mobili ci entrino perfettamente, mentre per misurare la distanza fra due città, la precisione del chilometro è persino eccessiva.
Per questo motivo si usa spesso, specialmente per quantificare la precisione, l’errore relativo espresso in percentuale, ottenuto dividendo l’errore assoluto per il valore vero. Più piccola la percentuale, più grande la precisione.