![[cml_media_alt id='219']Dieci piccioni in nove caselle[/cml_media_alt]](https://insight.stefanopaladini.net/wp-content/uploads/2012/10/TooManyPigeons-300x243.jpg)
Dieci piccioni in nove caselle
Il Principio della Piccionaia è un principio matematico che è noto anche come “principio dei cassetti” in Italia e analogamente “principe des tiroirs” in Francia, secondo il nome che utilizzò per la prima volta il matematico che lo esplicitò, Peter Gustav Lejeune Dirichlet, nel 1834 col nome Schubfachprinzip (“principio del cassetto”). Ma la denominazione anglosassone “pigeonhole principle” è decisamente più divertente, anche associata all’immagine che vedete in questa pagina, presa da wikipedia.
Ciò che rende affascinante questo principio matematico è il fatto che esso appare estremamente banale e intuitivo nella sua formulazione di base, ma la sua applicazione può risultare piuttosto difficile in casi più particolari e portare a risultati sorprendenti, inaspettati e spesso controintuitivi.
Facendo riferimento all’immagine in cima all’articolo, una formulazione immediata potrebbe essere: data una piccionaia con 9 caselle e 10 piccioni, ci sarà sicuramente una cella che contiene almeno 2 piccioni.
E fin qui… estremamente banale.
La formulazione banale di questo principio è così intuitiva che si può sfruttare per creare enigmi divertenti come questo.
Sei letti per sette viaggiatori
Una comitiva di 7 viaggiatori si presenta ad un albergo, e domanda un letto per ogni viaggiatore.
L’oste risponde: “Ho solo sei letti distinti colle lettere A, B, C, D, E, F. Ma guarderò di aggiustarvi.”
Perciò destinò:
due viaggiatori a dormire nel letto A,
poi uno nel letto B, e fa tre,
poi uno nel letto C, e conta quattro,
poi uno nel letto D, e conta cinque,
poi uno nel letto E, e conta sei;
poi prende uno di quelli che erano in A e lo conduce in F, e conta sette.
Così i 7 viaggiatori dormono in 6 letti, uno per letto.
Come ha fatto?
In questo esempio il nostro intuito urla che non è proprio possibile che 7 persone trovino posto in 6 letti, ciascuna da sola in un letto. Il principio della piccionaia si manifesta in maniera automatica e ci spinge a cercare il trucco nella formulazione dell’indovinello.
In effetti basta un poco di attenzione per rendersi conto che il settimo sfortunato viaggiatore è rimasto da solo nella hall dell’albergo mentre uno dei suoi amici nella stanza A veniva contato due volte.
Un utilizzo meno immediato dello stesso principio risale al 1624, quando Van Etten (al secolo Jean Leucheron) si propone di dimostrare che in una città di 150.000 abitanti vi sono due persone che hanno lo stesso numero di capelli.
Si stima che la superficie del capo umano portante capelli è di 775 cm2 e che ogni cm2 contiene al massimo 165 capelli, mediamente 150.
Quindi il massimo numero di capelli che può avere una persona è circa 775 * 165 = 123.875 < 150.000. In una città con più di un milione di abitanti, come Roma, la probabilità che due persone abbiano lo stesso numero di capelli è praticamente una certezza.
Formalmente, il principio afferma che se A e B sono due insiemi finiti e B ha cardinalità strettamente minore di A, allora non esiste alcuna da A a B.
Una versione generalizzata del principio afferma che se ci sono n oggetti discreti che devono essere allocati in m contenitori, allora ci sarà almeno un contenitore che conterrà almeno oggetti (il simbolo
denota la funzione soffitto).
Decisamente più interessamte è la generalizzazione probabilistica del principio. In questo caso possiamo dire che: se si mettono a caso n piccioni in una piccionaia da m posti con probabilità uniforme 1/m, allora almeno un posto della piccionaia conterrà più di un piccione con probabilità:
dove
Come potete vedere, con un’analisi approfondita, un principio così intuitivo porta ad una formulazione ben più complessa. Infatti ci sono casi in cui l’uso intuitivo di questo principio fallisce miseramente, (il che ci lascia intendere che il cervello ragiona in modo logico solo superficialmente), ma c’è bisogno di un’analisi più profonda.
Vediamo un caso in cui la formulazione rigorosa di cui sopra ci viene in aiuto nel risolvere un problema, noto come paradosso del compleanno, formulato nel 1939 da Richard von Mises.
Il paradosso dei compleanni
Supponiamo che, durante una festa con una trentina di partecipanti, un amico vi proponga di scommettere sul fatto che almeno due dei partecipanti facciano il compleanno nello stesso giorno.
Il nostro intuito ci porta ad applicare subito il principio della piccionaia: per avere la certezza che almeno due persone compiano gli anni nello stesso giorno, è necessario che vi siano almeno 367 invitati (tenendo conto anche degli anni bisestili). A questo punto il cervello abbandona la logica per adottare un criterio analogico: siccome il numero di commensali, abbiamo detto circa trenta, è molto lontano dal 367, che corrisponde alla probabilità del 100%, allora le probabilità che l’evento si verifichi sono molto scarse.
Quindi conviene scommettere contro… o no? Proviamo a fare un calcolo rigoroso.
Per effettuare il calcolo, si ricorre alla formula per la probabilità degli eventi indipendenti: per rendere più semplice il calcolo si assume che gli anni siano tutti di 365 giorni e che i compleanni siano equiprobabili, anche se ciò non è esatto. Aggiungere il giorno bisestile peggiora leggermente la probabilità, ma in compenso il fatto che i compleanni non siano equiprobabili la alza.
Calcoliamo dapprima la probabilità che nessuna data coincida, cioè calcoliamo la probabilità che tutte le date siano diverse. Prendiamo il primo invitato e vediamo la sua data di nascita, poi prendiamone un secondo. La probabilità che questi abbia una data di nascita diversa dal precedente è 364/365. Prendiamo un terzo invitato: la probabilità che il suo compleanno non coincida con nessuno dei due già considerati è 363/365… e così via fino, per esempio, al quarantesimo invitato la cui probabilità di essere nato in un giorno diverso dai 39 precedenti vale 326/365. Trattandosi di eventi indipendenti, questi numeri vanno moltiplicati tra loro per ottenere la probabilità che nessuna data di nascita coincida.
Se, in generale, il numero di partecipanti alla festa è p allora la probabilità che siano nati tutti e p in giorni diversi è:
Quindi, la probabilità che almeno due invitati siano nati lo stesso giorno è il suo complemento:
Se proviamo ad effettuare numericamente il calcolo di questa funzione e rappresentiamo graficamente il risultato traviamo il grafico che vediamo qui di fianco. Il valore della probabilità sale molto velocemente già con un numero di invitati abbastanza ridotto.
In effetti già con una festa di sole 24 persone si ha il 54% delle possibilità di vincere!
Già in un gruppo di 23 persone la probabilità è circa 0,51; con 30 persone essa supera 0,70, con 50 persone tocca addirittura 0,97, anche se per arrivare all’evento certo occorre considerare un gruppo di almeno 367 persone.
E’ dunque conveniente fare una scommessa a favore: la probabilità di vincere è decisamente alta!
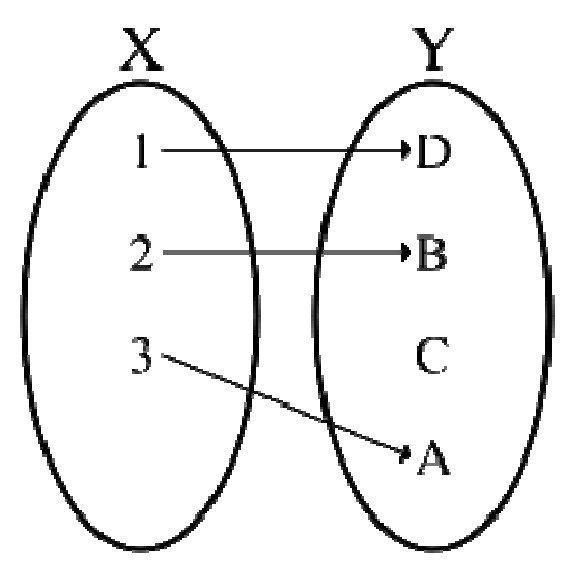 Una funzione si dice iniettiva se elementi distinti del dominio hanno un'immagine distinta, o equivalentemente se ogni elemento del codominio corrisponde al più ad un elemento del dominio.
Una funzione si dice iniettiva se elementi distinti del dominio hanno un'immagine distinta, o equivalentemente se ogni elemento del codominio corrisponde al più ad un elemento del dominio.Formalmente:
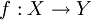 è iniettiva se
è iniettiva se 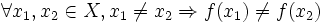
o equivalentemente: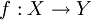 è iniettiva se
è iniettiva se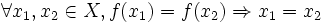
 -0
-0  )
)

Lascia un commento