Breve storia delle note musicali

Alcuni strumenti, come il trombone o il violino, permettono al musicista, facendo scorrere la coulisse o le dita sulle corde, di produrre una fluida progressione di suono, che varia dal più grave al più acuto, con continuità.
Eppure, come sappiamo, le note sono “solo 7”. Anziché una progressione continua abbiamo solo sette nomi, separati da intervalli discreti che si ripetono dal grave verso l’acuto.
Ma chi ha deciso quali debbano essere, fra le infinite possibili, le esatte frequenze che noi oggi identifichiamo con le 7 note? Perché proprio 7?
La risposta a queste domande è tutt’altro che semplice perché bisogna comprendere aspetti della fisiologia della percezione del suono, una buona dose di fisica e matematica e oltre mille anni di storia della musica, della filosofia e della religione, dall’antica Grecia ai giorni nostri!

Il suono e la sua percezione

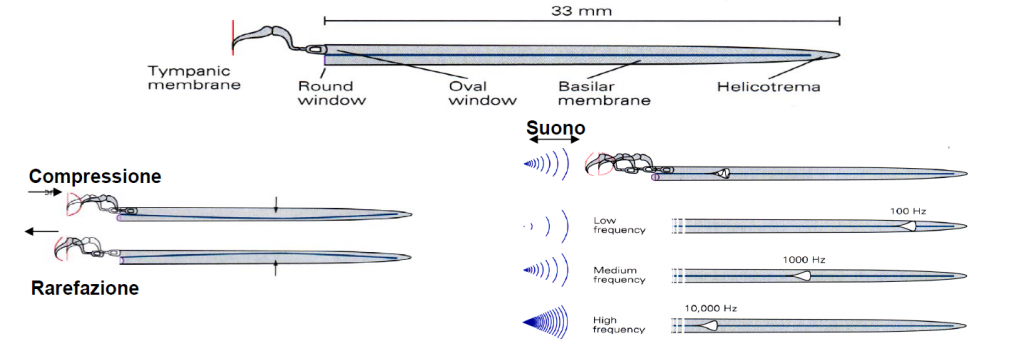
Nell’articolo sul funzionamento dell’orecchio interno, avevamo visto il modo in cui reagisce la membrana basilare all’interno della nostra coclea, quando viene investita da una vibrazione sonora, trasportata dall’esterno attraverso il timpano e la catena di ossicini.

L’aspetto notevole del funzionamento della membrana basilare è il fatto che su di essa la vibrazione, e quindi l’eccitazione delle cellule ciliate, è localizzata: nella zona più spessa, vicino la staffa e la finestrella ovale, le frequenze più acute, dalla parte opposta, dove la membrana è più sottile, le frequenze basse.

Quindi se il suono non è costituito da una frequenza pura, ma da una composizione di frequenze su uno spettro più o meno ampio, il nostro orecchio interno sarà in grado di scomporne le varie componenti e potrà percepirne l’intensità relativa alle diverse frequenze lungo diverse zone della membrana.

Ciò che è importante sottolineare in questa sede è che la membrana viene coinvolta nella sua interezza, non solo quando percepiamo una miscellanea di suoni provenienti da sorgenti diverse, come voci, strumenti musicali, rumori ambientali e quant’altro, ma anche se ascoltiamo una una singola nota, prodotta da un singolo strumento musicale. Questo perché quella nota, prodotta dalla vibrazione di un mezzo fisico, è in realtà un fenomeno a cui partecipano oscillazioni elementari a varie frequenze.

Le “oscillazioni elementari” di cui sopra, vengono denominate in gergo più tecnico, sia musicale che matematico: armoniche. Per capire più nel dettaglio di cosa si tratti è utile studiare un sistema molto semplice, o meglio la rappresentazione ideale di un sistema molto semplice: una corda vibrante.

I primi esperimenti pratici con i modi di vibrare di una corda, come vedremo più avanti, risalgono al 500 a.C. e vengono attribuiti a Pitagora e i suoi seguaci, ma per i fisici e i matematici, per arrivare a capire a fondo il fenomeno, è necessario scomodare un’equazione dall’aspetto un po’ intimidatorio, come la seguente.

Si tratta dell’equazione di un’onda unidimensionale, ed è quella che fa al caso nostro se vogliamo studiare una corda ideale, in cui la sezione trasversale è trascurabile rispetto alla lunghezza, in cui un segmento della corda applica al successivo solo sforzi di tensione (quindi niente flessioni e torsioni) e in cui la densità è costante lungo tutta la lunghezza.
In questa equazione si descrive con la coordinata u lo spostamento trasversale di ogni punto della corda lungo la coordinata x e nel tempo t. Il parametro v rappresenta la velocità di propagazione dell’onda lungo la corda.

Considerando tutte le ipotesi semplificative di cui sopra e supponendo che la nostra corda sia vincolata alle estremità, i matematici ci dicono che la suddetta equazione ha come soluzione una somma infinita di sinusoidi oscillanti.
L’immagine sopra mostra come una vibrazione generica di una corda può essere interpretata come diverse vibrazioni sinusoidali pure, ciascuna con la propria ampiezza, che si sommano fra loro a frequenze via via crescenti e multipli di una frequenza fondamentale proporzionale alla tensione T e inversamente proporzionale alla densita μ.
Per una corda di lunghezza L ci saranno quindi tanti modi di vibrare a frequenza crescente con n=1,2,3… e inversamente proporzionali alla sua lunghezza:

Una volta compreso il comportamento della corda ideale è facile rendersi conto che anche le corde reali si comportano in maniera simile. Il legame fra tensione, densità e lunghezza di cui sopra coincide con l’esperienza comune che ci dice che una corda più sottile o più tesa produce un suono più acuto di una corda più spessa e più lasca o più lunga.

Tramite computer e oscilloscopi, possiamo facilmente constatare anche che scomponendo le frequenze fondamentali che compongono il suono complesso di una corda, esse stanno fra loro effettivamente in rapporti interi, almeno per le prime componenti, che sono quelle a maggiore intensità. Al crescere della frequenza infatti cresce anche l’energia necessaria per deformare fisicamente la corda per cui nel caso reale, la rigidezza meccanica fa sì che gli armonici superiori siano via via meno intensi e di fatto le sinusoidi che compongono l’oscillazione, non sono infinite.

Le corde più spesse, quelle che producono le note più gravi, proprio a causa della loro sezione maggiore, sono anche più lontane dal modello ideale di corda filiforme e infatti, tramite la strumentazione, possiamo constatare che le loro armoniche tendono ad allontanarsi leggermente dalla perfetta progressione fatta di multipli esatti. La cosa non sfugge neanche al nostro orecchio, che ci fa percepire le note più basse del pianoforte con una caratteristica più “metallica” rispetto al suono più puro delle corde più acute.

Il fatto accennato prima, che la membrana basilare della nostra coclea sia in grado di scomporre le componenti in frequenza di un suono complesso, è ciò che ci permette di distinguere la qualità del suono, per esempio distinguere il suono di un pianoforte da quello di una chitarra anche quando suonano la stessa nota. E quando ascoltiamo due note suonate contemporaneamente, l’orecchio ci restituisce una sensazione “gradevole” quando le frequenze armoniche stanno fra loro in rapporti semplici, perché le armoniche vanno ad eccitare zone della membrana che si sovrappongono.