Breve storia delle note musicali

Limitazioni delle accordature storiche

Nonostante la forte spinta ideologica a favore della dottrina pitagorica favorisse l’utilizzo della scala musicale ad essa associata, per lo meno in ambito ecclesiastico, essa presentava dei problemi a cui abbiamo accennato in chiusura del paragrafo ad essa dedicato.
Nel periodo in cui la cultura musicale era prevalentemente orientata al canto monofonico al massimo arricchito da voci addizionali ma vincolate da rigide regole nella scelta degli intervalli, l’utilizzo della scala pitagorica non presentava particolari controindicazioni.
I problemi si palesavano se si cercava di ottenere soluzioni più ricche in termini di parti sia vocali che strumentali suonate contemporaneamente.

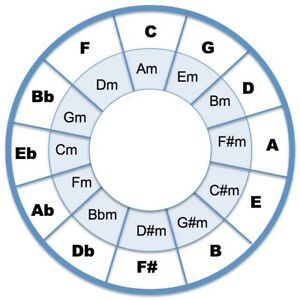
Quello che si vede rappresentato nell’immagine è il circolo delle quinte così come lo conosciamo e usiamo ancora oggi, in notazione moderna. In esso vi sono dodici toni ciascuno separato da un intervallo di quinta e si può vedere che, partendo dal Do, in dodici salti, la nota di arrivo è nuovamente un Do, portando a dodici il numero massimo di note necessarie a chiudere il circolo.
Purtroppo però, questa elegante costruzione non sta in piedi matematicamente.

La generazione della nota successiva nel circolo delle quinte corrisponde a moltiplicare la frequenza della nota di partenza per 3/2, per definiziome di intervallo di quinta. In altre parole, se la nota di partenza fosse il Do e questo avesse frequenza 1Hz (per semplificare), la nota successiva Sol avrebbe frequenza 1.5Hz cioè 1 x (3/2). La nota successiva al Sol, che oggi chiamiamo Re, sarà (3/2) x (3/2) cioè (3/2)² che fa 2,25 quindi essendo più del doppio del Do di partenza sarà nell’ottava successiva. Ripetendo questo procedimento per tutti i dodici gradi del circolo si ottiene (3/2)¹²=129.7 che dovrebbe essere di nuovo un Do, sette ottave più in alto.
Per definizione di ottava, però, il Do sette ottave più in alto dovrebbe avere una frequenza pari a quella del Do iniziale, raddoppiata per sette volte. Sfortunatamente per Pitagora, 2⁷ vale 128 che, anche se vicino, è diverso da 129.7!
In particolare il rapporto fra il Do che si otterrebbe per salti di quinta e quello che si otterrebbe per salti di ottava prende il nome di comma pitagorico e vale 1.0136.

E di comma non ne esiste solo un tipo!
La scala pitagorica aveva due grandi vantaggi, l’uniformità, in quanto i rapporti fra due note successive erano sempre o di 9/8 (tono) o di 256/243 (semitono) e il fatto che gli intervalli di ottava, quarta e quinta fossero perfettamente consonanti. I problemi nascevano quando si provava ad usare altri intervalli o si costruivano intervalli come terze, cioè un Do insieme ad un Mi, e seste, cioè un Do insieme ad un La.

Un’alternativa alla scala pitagorica fu proposta già nell’antichità da un altro filosofo pitagorico, successivo a Pitagora: Archita.
Archita cercò di superare le limitazioni della scala pitagorica ammettendo di poter suddividere l’ottava utilizzando anche altri divisori, includendo rapporti con 2, 3, 4 e 5.
Le sue teorie furono poi riprese da Tolomeo nel II secolo d.C. e infine da Gioseffo Zarlino nel 1558.

La scala tolemaica prevedeva la costruzione degli intervalli utilizzando rapporti fatti da numeri piccoli, quindi oltre ai 4/3 e 3/2 per quarta e quinta della scala pitagorica, avremo anche 5/4 e 5/3 per terza e sesta anziché 81/64 e 27/16, la seconda viene ottenuta come per Pitagora da 9/8 e la settima vale semplicemente 15/8 anziché 243/128.

Il risultato è una scala in cui anche gli intervalli di terza e sesta sono gradevoli all’orecchio, cioè perfettamente consonanti.
Il motivo è facilmente comprensibile se consideriamo quanto esposto nel primo paragrafo. Nella scomposizione di un suono nei suoi armonici naturali, si trovano tutti i multipli interi della frequenza fondamentale. Quindi prendendo un multiplo intero e dividendolo per due quanto basta per riportarlo nell’ottava fondamentale si ottiene, con qualche approssimazione, proprio la scala tolemaica, che per questo motivo è detta anche scala naturale.
Tutto risolto? Purtroppo no!

La scala tolemaica se anche introduce delle note che suonano bene insieme, ottiene questo risultato modificando le ampiezze dei vari intervalli, che ora non sono più solo due, tono e semitono, come per la scala pitagorica, ma ora il tono stesso può essere grande o piccolo e non tutti gli intervalli di quinta sono perfetti. Come conseguenza, anche per la scala naturale si verifica un fenomeno simile a quello visto per la scala pitagorica.

Se partiamo dal Do e saliamo di un intervallo di sesta (moltiplichiamo per 5/3) per trovare la nota La e poi saliamo ulteriormente di una quarta (moltiplichiamo per 4/3) troviamo un Re nell’ottava successiva.
Ma se da questo Re proviamo a scendere di una quinta (dividiamo per 3/2) trovando un Sol e poi scendiamo ulteriormente di una quinta dovremmo trovare il Do di partenza. Invece troviamo una nota che è leggermente più bassa di una quantità detta comma zarliniano (circa 0.988, facendo il conto 80/81)

Per fortuna, come vedremo nel prossimo paragrafo, c’è un modo per mettere d’accordo tutti… più o meno.