Dal paradosso del sorìte alla frontiera frattale

La risposta fuzzy

Recentemente il problema di gestire a livello formale le situazioni descritte nel paragrafo precedente è stato affrontato da diversi studiosi e generalmente si inizia a parlare formalmente di logica fuzzy, o in questo caso di insiemi fuzzy (spesso chiamati “sfumati” in italiano), grazie al lavoro del matematico iraniano Lotfi Asker Zadeh il quale li descrisse per la prima volta nel 1964.
L’obiettivo della logica fuzzy è quello di superare la limitazione della logica classica di riferirsi solo ai due estremi della realtà, vero o falso, trascurando il fatto che le variabili reali sono generalmente delle grandezze che possono assumere infiniti valori in un campo di variazione.
Queste grandezze sono le grandezze vaghe.
Ho indossato un grande cappello; Maria è un po’ chiaccherona; oggi ho poca fortuna.
In tutti questi esempi abbiamo fatto uso di modificatori (grande, un po’, poca) che sono campanelli d’allarme della presenza di nozioni vaghe.
Se infatti può essere ben identificato il fatto che il cappello venga o non venga indossato, che Maria sia in grado di parlare o che io possa vincere a poker, è decisamente difficile definire quanto sia grande il mio cappello, o il flusso di parole che esce dalla bocca di Maria o peggio ancora se un tris d’assi in una mano di poker sia un punteggio vincente o no!

Questo problema dell’identificare i concetti vaghi non è esclusivo dei casi della vita quotidiana, in quanto anche nella scienza più esatta siamo costretti ad averci a che fare.
Per esempio tutti i teoremi della meccanica classica sono rigorosamente sbagliati in quanto non tengono conto delle correzioni portate dalla meccanica relativistica. Ma noi sappiamo anche che, a velocità piccole rispetto alla velocità della luce, tali effetti non sono avvertibili. E quindi possiamo felicemente continuare ad usare la meccanica classica come se nulla fosse.
Ma quanto piccole?
Ancora una volta un concetto vago, per il quale, a rigore, dovremmo dare una definizione.

La logica fuzzy fornisce i mezzi per operare con grandezze che possono avere valori qualsiasi all’interno di una scala. Cerchiamo di capire di cosa si tratta con un esempio.
Vogliamo costruire un termostato intelligente e fornirlo di una logica di funzionamento che gli permetta di distinguere tre livelli di temperatura: alta, media e bassa.
Un approccio logico tradizionale porta a definire in maniera precisa questi assiemi. Per esempio: temperatura bassa sotto i 15°C, temperatura media fra 15°C e 25°C e temperatura alta sopra i 25°C.
Come dovrà comportarsi il termostato nel caso in cui la temperatura sia di soli 25.1°C?
Non ha senso considerare “alta” questa temperatura eppure è proprio ciò che farebbe il nostro termostato in base alle definizioni date.
Per superare questo ostacolo dobbiamo abbandonare l’idea che un valore di temperatura appartenga esclusivamente ad uno dei tre insiemi, ma possa avere un “grado di appartenenza“, compreso fra 0 e 1, diverso per ogni assieme. Questo viola espressamente il “” della logica tradizionale. Nell’esempio precedente, la temperatura di una stanza a 19°C potrebbe appartenere con un grado di verità di 0.8 alla temperatura media e di 0.2 alla temperatura calda.
Schematicamente possiamo rappresentare la situazione come segue.

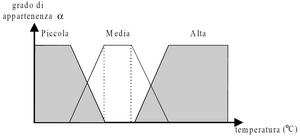
L’insieme delle temperature basse conterrà nella sua definizione anche la funzione di appartenenza, che sopra abbiamo rappresentato con un grafico. Così per gli altri assiemi, che in questo modo non sono più assiemi nel senso tradizionale, ma diventano assiemi “fuzzy”.

Anche nella logica è necessario fare degli aggiustamenti per poter gestire questi nuovi oggetti sfumati.
I tradizionali operatori AND, OR e NOT si ridefiniscono come segue:

NOT x = (1-v(x))
x AND y = min (v(x), v(y))
x OR y = max (v(x), v(y))

Dove con v(x) abbiamo indicato la funzione di appartenenza, applicata alla grandezza x.

Quindi il problema della linea di demarcazione fra calvo e capelluto con cui Eubulide metteva in crisi la logica aristotelica, viene spalmato in una linea sfumata tramite la funzione di appartenza.

Certo, in partenza noi abbiamo dei valori ben precisi di temperatura e in uscita il nostro termostato dovrà essere acceso o spento. Senza ambiguità.
Questi valori sono detti “crisp” nel gergo della logica fuzzy.
Quindi è necessario prevedere delle funzioni di fuzzificazione in ingresso e di defuzzificazione in uscita, che permettano di far dialogare i due mondi e trasformare i valori crisp in valori fuzzy e viceversa.
Il vero passo avanti, rispetto all’approccio tradizionale è che, nel defuzzificare i risultati di un’elaborazione fuzzy, si possono usare funzioni che considerino l’intero insieme fuzzy risultante dall’elaborazione.
Per dare un’idea, degli svariati metodi utilizzati, cosideriamo il metodo del baricentro mostrato in figura.

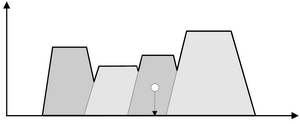
Con questo metodo, si considera, come valore crisp in uscita, il baricentro dell’area complessiva creata dalle singole funzioni di appartenenza delle diverse variabili in ingresso, dopo essere state manipolate opportunamente dall’elaborazione.