Il bottino della discordia

Tre pericolosi criminali, Aldo, Bruno e Carlo, riescono a portare a termine un grosso colpo ad una gioielleria.
Quando tornano al loro rifugio segreto con il bottino, tuttavia, sorgono i problemi, in quanto i tre non riescono a mettersi d’accordo su come dividere il maltolto in modo che ciascuno sia soddisfatto dalla propria parte.
Siete in grado di proporre una soluzione?

Quella prospettata in questo articolo è una versione un po’ più “cinematografica” di un problema su cui i matematici stanno lavorando per lo meno dagli anni ’40: il problema del taglio della torta.
Ritornando al nostro caso, non si tratta semplicemente di dividere il bottino fra i tre malfattori, ma bisogna fare in modo che ciascuno sia contento della parte ricevuta, onde evitare che la situazione degeneri violentemente. Ciò che complica la suddivisione è il fatto che il bottino è eterogeneo, composto da gioielli, pietre e metalli preziosi, oggetti d’arte, raffinata manifattura e quant’altro, e ciascun ladro attribuisce valori diversi ai vari oggetti, in base a dei criteri strettamente personali.
Mettere tutti d’accordo sembra un impresa impossibile!

Eppure una soluzione al caso più semplice, quello con due soli “agenti”, la troviamo addirittura nella Bibbia quando Abramo divide la terra di Canaan in due parti e lascia a Lot la facoltà di scegliere.

⁸Abram disse a Lot: «Non vi sia discordia tra me e te, tra i miei mandriani e i tuoi, perché noi siamo fratelli. ⁹Non sta forse davanti a te tutto il territorio? Sepàrati da me. Se tu vai a sinistra, io andrò a destra; se tu vai a destra, io andrò a sinistra».
Genesi 13 – Testo CEI 2008

Ovviamente, avere a che fare con più di due soggetti complica notevolmente la procedura. Quella che vediamo nel seguito è la soluzione scoperta indipendentemente negli anni ’60 dai due matematici John Selfridge e John Horton Conway relativa al caso di 3 agenti, ma nel 2017 Haris Aziz e Simon Mackenzie hanno proposto una soluzione discreta e limitata, valida per un numero arbitrario di persone, anche se, ad onor del vero, al crescere del numero di persone, il numero di suddivisioni del bottino diventa astronomico.

La suddivisione del bottino

Il primo ad iniziare la suddivisione è Aldo.

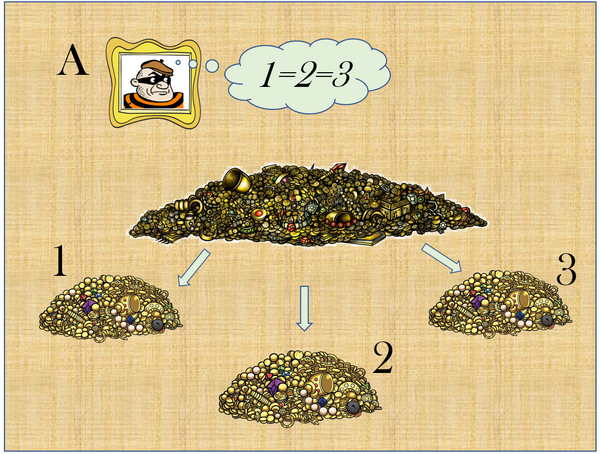
Il suo compito è di creare tre mucchi di gioielli a partire dal bottino totale facendo in modo che il loro valore sia quanto più simile possibile. Ovviamente dal suo punto di vista.
Possiamo dire che, per quanto riguarda Aldo, se dovesse scegliere lui uno dei tre mucchi, non farebbe nessuna differenza uno qualsiasi di essi. Inoltre Aldo non avrebbe nessuna invidia nei confronti dei propri compagni se questi ricevessero uno qualsiasi degli altri mucchi, o parti di essi.
Per inciso, ho usato il termine invidia per richiamare l’espressione inglese che viene usata per descrivere questa procedura di suddivisione: “envy-free” cioè “senza invidia“.
Nonostante i mucchi fatti da Aldo abbiano per lui valore uguale, supponiamo che dovendo sceglierne uno, egli segua un ordinamento ben preciso, per esempio prima l’1, poi il 2 e poi il 3.
Ma prima di reclamare la sua parte, Aldo dovrà attendere che anche gli altri abbiano fatto le loro scelte.

Il secondo ad agire sui mucchi del bottino è Bruno.

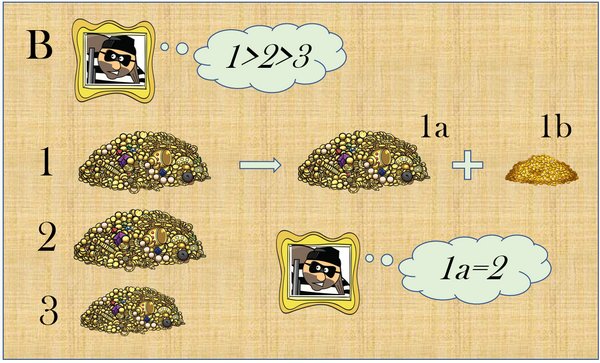
A Bruno vengono presentati i tre mucchi preparati da Aldo, ma ovviamente per lui, in base alla propria scala di valori, essi non saranno affatto equivalenti l’uno con l’altro.
Supponiamo che agli occhi di Bruno il primo sia più ricco del secondo e questo del terzo.
Si chiede a Bruno di sottrarre al mucchio 1 una parte di bottino in modo tale che il mucchio risultante, che chiameremo 1a, abbia lo stesso valore del gruppo 2. Il resto, che chiameremo 1b, per ora lo mettiamo da parte.
Dopo la suddivisione operata da Bruno i tre gruppi saranno: 1a, 2 e 3, e a gli occhi di Bruno 1a e 2 saranno perfettamente equivalenti, con le stesse considerazioni fatte per Aldo, mentre il gruppo 3 sarà un po’ più scarso.
Agli occhi di Aldo invece sarà 1a ad essere più scarso perché gli è stata sottratta una porzione.
Bruno sarebbe quindi perfettamente contento di ricevere sia 1a che 2 e non avrebbe niente in contrario che gli altri ricevano uno qualsiasi dei mucchi perché nessuno riceverà un mucchio più ricco del suo. Dovendo scegliere fra 1a e 2, come per Aldo, Bruno sceglierà comunque 1a.

Adesso tocca a Carlo.

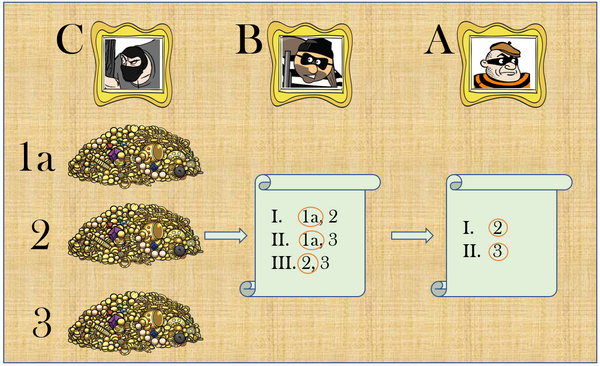
Finalmente Carlo non opera nessuna suddivisione ma si limita a scegliere la parte di bottino che secondo lui è la migliore.
La scelta è fra 1a, 2 e 3, e la cosa importante da notare è che, qualunque sia la scelta operata da Carlo, fra i due gruppi rimanenti (che possono essere [1a,2] oppure [1a,3] oppure [2,3]) ci sarà sempre almeno un mucchio che uno dei suoi compagni considera migliore o al massimo equivalente a quelli che spetterebbero agli altri.

A questo punto il gioco è fatto, perché il prossimo ad entrare in azione sarà Bruno, che sceglierà o 1a o 2, in quest’ordine. Infine Aldo riceverà il mucchio rimanente, che sarà o 2 o 3, ma per Aldo, come abbiamo visto, l’uno o l’altro è perfettamente accettabile.

Rimane da sistemare il rimasuglio che avevamo chiamato 1b.

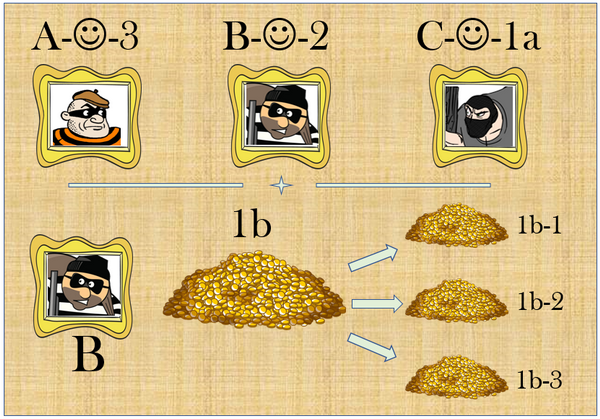
L’onere spetta a colui che NON ha scelto il mucchio 1a.
Nel nostro esempio, supponiamo che sia Carlo ad aver scelto 1a, quindi, per i giochi di preferenze che abbiamo indicato, Bruno avrà scelto 2 e Aldo avrà ricevuto 3.
Spetterà quindi a Bruno occuparsi di 1b e tutto ciò che dovrà fare sarà suddividerlo ancora in tre parti tali che, secondo lui, siano equivalenti.
La scelta adesso ritorna a Carlo che sceglierà uno fra i tre mucchietti 1b-1, 1b-2 o 1b-3 e sarà soddisfatto in quanto potrà scegliere la parte che secondo lui è la migliore da aggiungere ad un malloppo che già considerava soddisfacente.

Poi tocca ad Aldo che sceglie uno fra i due mucchietti rimasti ed è importante considerare nel dettaglio il punto di vista di Aldo.
Ricordiamo che Aldo, ora in possesso del mucchio 3, era quello che aveva creato i tre mucchi iniziali e, dal suo punto di vista, essi erano perfettamente equivalenti. In particolare 3 era equivalente a 1 quando 1 era completo.
Carlo aveva scelto il gruppo 1a che era stato decurtato e ora è in possesso di 1a più una parte di ciò che gli era stato tolto. Quindi Carlo è in possesso di una quantità sicuramente minore di 1 e di conseguenza di 3.
Per utilizzare la terminologia usata ad Aziz e Mackenzie, diremo che Aldo è dominante rispetto a Carlo in quanto non proverebbe invidia neanche se a questi venisse assegnato tutto il mucchietto 1b.
Invece Bruno è in possesso del mucchio 2 che, per Aldo, è equivalente al 3.
Ma siccome è Aldo che sta operando la sua scelta, fra i due mucchietti superstiti sceglierà il migliore quindi a Bruno, che ha un mucchio equivalente al suo, lascerà il mucchietto più scarso.

Infine Bruno, che non effettua nessuna scelta, riceverà ciò che gli viene lasciato dagli altri e sarà comunque soddisfatto perché è stato lui a fare la suddivisione di 1b e le tre parti ai suoi occhi erano equivalenti dal principio.

Un’ultima considerazione: il fatto di obbligare l’agente che effettua la seconda suddivisione (Bruno nel nostro caso) a scegliere di preferenza il mucchio da lui diviso, non toglie generalità alla procedura, ma serve solo ad avere una sequenza di ritorno (Carlo, Bruno, Aldo) sempre uguale indipendentemente dalla scelta di Carlo.
Altrimenti si dovrebbe passare la palla ad Aldo anziché Bruno a seconda che Carlo scelga o meno il mucchio 1a, in maniera analoga a ciò che si fa per decidere a chi spetta l’onere di suddividere 1b nell’ultima fase della procedura.