Il Sistema Internazionale com’è oggi

Nel corso degli anni, dall’originale formulazione del sistema MKS, si è evoluto un sistema di unità di misura sempre più completo e preciso.
Le prime unità di misura ad essere standardizzate furono, come abbiamo detto, il metro, il chilogrammo e il secondo, ma presto vi si affiancarono altre unità necessarie a rappresentare grandezze in uso nelle varie branche della fisica.
Le unità di misura fondamentali con le grandezze ad esse associate furono le seguenti.

  • metro (m) – lunghezza
  • chilogrammo (kg) – massa
  • secondo (s) – tempo
  • ampere (A) – corrente elettrica
  • kelvin (K) – temperatura termodinamica
  • mole (mol) – quantità di sostanza
  • candela (cd) – intensità luminosa

La dimensione effettiva di una quantità unitaria di una delle grandezze era considerata pari a quella di un Campione Materiale, conservato in condizioni estremamente controllate presso il BIPM e realizzato in materiale scelto per essere nel tempo il meno suscettibile possibile ad alterazioni chimico-fisiche.
Tale procedura rappresentava però il vero tallone d’Achille di tutto l’impianto normativo in quanto il comitato scientifico era ben consapevole dell’instabilità apportata al sistema dal fatto di dover fare affidamento a dei campioni fisici.
Nell’immagine sotto si può vedere il campione di chilogrammo, un cilindro di platino-iridio di diametro e altezza entrambi pari a 39mm, conservato sottovuoto a Sévres in Francia, con un grafico che rappresenta il confronto fra la sua massa e quella dei campioni primari da esso derivati e conservati presso gli istituti metrologici di vari paesi.

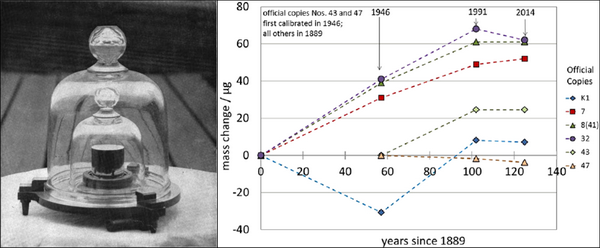
La variabilità evidenziata dal grafico è conseguenza del fatto che l’unità fondamentale è basata su un campione fisico, suscettibile di alterazioni nel tempo.

Per questo motivo, negli anni, sono stati studiati uno dopo l’altro, dei modi per svincolare la definizione delle varie unità dall’esistenza di un campione materiale per legarla alla dimensione di una qualche costante universale, finché il 20 maggio 2019, proprio con la ridefinizione del chilogrammo, tutte le grandezze fondamentali e unità di misura ad esse collegate, sono state messe in correlazione con delle proprietà fondamentali dell’universo.
Oggi il Sistema Internazionale non è più basato su 7 unità fondamentali, ma su 7 costanti universali il cui valore è stato fissato senza incertezza e dalle quali si possono fare derivare le unità di misura.
Fra di esse ne troviamo qualcuna che non è particolarmente conosciuta al di fuori degli ambiti più specialistici, come la costante di Planck ℎ, che rappresenta la costante di proporzionalità fra energia E e frequenza ν: E=ℎν, e la costante di Boltzmann che rappresenta la costante di proporzionalità fra energia e temperatura: E=kT.

  • La frequenza di transizione iperfine dello stato fondamentale dell’atomo di cesio 133, ΔνCs, è 9 192 631 770 Hz (hertz).
  • La velocità della luce nel vuoto, c, è 299 792 458 m/s (metri al secondo).
  • La costante di Planck, ℎ, è 6,62607015 x 10-34 J*s (joule secondo=kg m2 s-1).
  • La carica elementare, e, è eguale a 1,602 176 634 x 10-19 coulomb (A s).
  • La costante di Boltzmann, k, è 1,380 649 x 10-23 J/K (joule al kelvin).
  • La costante di Avogadro, NA, è 6,022 140 76 x 1023 mol-1 (mole-1).
  • L’efficienza luminosa, Kcd, della radiazione monocromatica di frequenza 540*1012Hz è 683 lm/W (lumen per watt).

Utilizzando questo approccio, la definizione delle unità di misura diventa più che altro una descrizione del metodo per ricavarle, sfruttando fenomeni fisici che dipendono dalle suddette costanti.
Di seguito le definizioni ufficiali.

Misura dell’intervallo di tempo, il secondo – Δν

Per definire un intervallo di tempo standard si è cercato un fenomeno naturale la cui durata fosse costante in qualsiasi situazione.

Il secondo è la durata di 9 192 631 770 periodi della radiazione corrispondente alla transizione tra due livelli iperfini dello stato di base dell’atomo di Cesio 133.

Misura della lunghezza, il metro – c Δν

Una volta definita la durata di 1 secondo è possibile sfruttare un’altra costante naturale, la velocità della luce, per ricavare l’unità di misura della lunghezza.

Il metro è la lunghezza del percorso computo da un raggio di luce nel vuoto in un intervallo di tempo pari a 1/299 792 458 s

Misura della massa, il chilogrammo – ℎ c Δν

Il chilogrammo storicamente è stata l’ultima unità di misura ad essere stata definita in termini di costanti fondamentali. Nella sua definizione, oltre alla frequenza e la velocità della luce di cui sopra, rientra la costante di Plank.

Il chilogrammo è definito a partire dal valore numerico fisso della costante di Planck h, pari a 6,626 070 15 ×10−34 quando espressa nell’unità J s, che corrisponde a kg m2 s−1.

\displaystyle 1kg=\left ( \frac{h}{6,626\, 070\, 15\cdot 10^{-34}} \right )m^{-2}s

\displaystyle 1kg=\frac{(299\, 792\, 458)^{2}}{(6,626\, 070\, 15\cdot 10^{-34})(9\, 192\, 631\, 770)}\frac{h\Delta \nu _{Cs}}{c^{2}}\approx 1,475\, 521\, 4\cdot 10^{40}\frac{h\Delta \nu _{Cs}}{c^{2}}

Misura della corrente, l’Ampere – e Δν

Per definire l’unità di misura della corrente si utilizza un’altra costante fondamentale della natura, la carica dell’elettrone e che viene fissata pari a 1,602 176 634 x10-19A s.
Dalla definizione si ricava:

\displaystyle 1A=\left ( \frac{e}{1,602\, 176\, 634\cdot 10^{-19}} \right )s^{-1}

e, esprimendo il tutto in termini di costanti universali:

\displaystyle 1A= \frac{1}{(9\, 192\, 631\, 770)(1,602\, 176\, 634\cdot 10^{-19})} e\Delta \nu _{Cs}\approx 6,789\, 687\cdot 10^{8}\Delta \nu _{Cs}e

Misura della temperatura, il Kelvin – k h Δν

Per definire l’unità di temperatura si introduce un’ulteriore costante universale, la costante di Boltzmann k che lega fra loro temperatura ed energia e che viene fissata pari a 1,380 649 x10-23 J K-1.
Ricordando che il Joule è un’unità derivata pari a m2 kg s-2, si può ricavare:

\displaystyle 1 K=\left ( \frac{1,380\, 649}{k} \right )\cdot 10^{-23}kg m^{2}s^{-2}

e in termini di costanti universali:

\displaystyle 1 K= \frac{1,380\, 649\cdot 10^{-23}}{(6,626\, 070\, 15\cdot 10^{-34})(9\, 192\, 631\, 770)} \frac{\Delta \nu _{Cs}h}{k}

Misura della quantità di sostanza, la mole – NA

Per definire la mole, unità di misura della quantità di sostanza, è sufficiente basarsi sulla definizione del Numero di Avogadro definito pari a 6,02214076 x1023.
Una mole è una quantità di sostanza che contiene un numero di quantità elementari pari al Numero di Avogadro.
In formule:

\displaystyle N _{A}=6,022\, 140\, 76^{23}mol^{-1}

da cui:

\displaystyle 1mol=\left ( \frac{6,022\, 140\, 76\cdot 10^{23}}{N_{A}} \right )

Misura dell’intensità luminosa, la candela – KcdhΔν

Per definire la candela cd, unità di misura dell’intensità luminosa, è necessario introdurre l’ultima costante universale, l’efficienza luminosa Kcd.
Si fissa il valore dell’efficienza luminosa della radiazione monocromatica di frequenza 540×1012Hz pari a 683 lumen per watt.
Il lumen e il watt sono a loro volta delle unità di misura derivate che possono essere ricondotte alle unità fondamentali fin qui definite.
Dalla definizione di candela si ottiene:

\displaystyle 1\, cd=\left ( \frac{K_{cd}}{683} \right )kg\, m^{2}s^{-3}sr^{-1}

e, sostituendo i valori delle costanti:

\displaystyle 1\, cd= \frac{1}{(6,626\, 070\, 15\cdot 10^{-34})(9\, 192\, 631\, 770)(683))} (\Delta \nu _{Cs})^{2}hK_{cd}\approx

\displaystyle \approx 2,641\, 830\cdot 10^{10}(\Delta \nu _{Cs})^{2}hK_{cd}

←

→

Pagine: 1 2 3 4 5