Le unità di Plank

Come abbiamo visto il Sistema Internazionale consiste un insieme di unità di misura coerenti fra loro, definite in modo da poter essere generate l’una dall’altra senza introdurre fattori moltiplicativi diversi da 1 o opportune potenze di 10.
Quindi, per fare un esempio, se si vuol sapere qual è la definizione dell’unità di misura per la pressione, il Pascal, lo si può ricavare sapendo che la pressione è una forza per unità di superficie, che nel S.I. si misurano in Newton e metri quadrati, quindi 1 Pascal sarà uguale a 1 Newton diviso 1 metro quadrato.
Questa eleganza e semplicità vale per tutte le unità di misura del sistema, ma non per le costanti fondamentali che, come abbiamo visto, hanno dei valori particolarmente astrusi e arbitrari.
Il motivo, come è facile immaginare, risiede nel fatto che i valori delle costanti riflettono le origini storiche e puramente antropocentriche che hanno portato alla definizione delle unità di misura.

L’eredità del metro come frazione del meridiano terrestre, o del secondo come frazione del periodo di rotazione della Terra, hanno vincolato la scelta dei valori delle costanti universali per far sì che le unità risultanti avessero la dimensione a cui le popolazioni sono abituate. Il risultato è che oggi esse hanno dei valori che hanno senso solo per una particolare razza di animali senzienti che abitano un particolare pianeta roccioso fra gli innumerevoli presenti nell’universo.

Nel 1899, il già citato fisico tedesco Max Planck, propose un sistema di unità di misura che fosse veramente universale perché basato sulle proprietà dello spazio libero, quindi che non facesse riferimento a nessuna sostanza particolare, valori particolari di gravità o intensità luminosa ecc. Un sistema che fosse comprensibile a qualunque intelligenza che avesse una comprensione sufficientemente profonda delle leggi naturali.
Quello che propose Planck non è diverso, operativamente, da ciò che è stato fatto dopo di lui nella revisione del Sistema Internazionale, tuttavia la sua proposta andava oltre il semplice basare le unità sulla definizione delle costanti universali, ma proponeva di sceglierle in modo che tali costanti valessero 1!
Egli chiamò “naturali” le unità di misura che ne derivano e le cinque costanti fondamentali da lui scelte furono:

  • la velocità della luce nel vuoto, c, (nota anche come velocità di Planck)
  • la costante gravitazionale, G
  • la costante ridotta di Planck, ℏ (dove ℏ=ℎ/2π,nota anche come azione di Planck)
  • la permittività del vuoto, ε0 (nota anche come permittività di Planck)
  • la costante di Boltzmann, kB (nota anche come capacità termica di Planck)

Le cinque unità di misura naturali che derivano dalla scelta di queste costanti sono dette “di Planck” e si può calcolare quanto varrebbero se fossero espresse nel Sistema Internazionale:

\displaystyle l_{P}=\sqrt{\frac{ \hbar G}{c^{3}}}\approx 1,6\cdot 10^{-35}m

\displaystyle m_{P}=\sqrt{\frac{\hbar c}{ G}}\approx 2,2\cdot 10^{-8}kg

\displaystyle t_{P}=\sqrt{\frac{ \hbar G}{c^{5}}}\approx 5,4\cdot 10^{-44}s

\displaystyle q_{P}=\sqrt{4\pi \epsilon _{0}\hbar c}\approx 1,9\cdot 10^{-18}C

\displaystyle \Theta _{P}=\sqrt{\frac{\hbar c^{5}}{ Gk_{B}^{2}}}\approx 1,4\cdot 10^{32}K

Come si può vedere, i valori che si ottengono sono enormemente piccoli o enormemente grandi.
Nell’immagine sotto si può avere un’idea di quanto la lunghezza di Planck sia piccola rispetto ad alcun oggetti di riferimento.

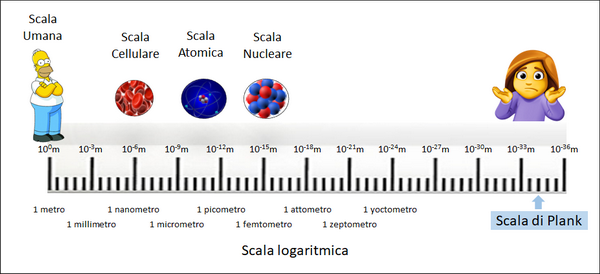
Per tale motivo inizialmente molti fisici criticarono l’idea delle unità di Planck vista la loro pressoché nulla utilità pratica.
L’importanza delle unità di Planck iniziò però ad emergere nel corso degli anni man mano che le teorie fisiche hanno iniziato ad affinarsi nel tentativo di individuare una teoria unificata che descriva tutte le interazioni fondamentali.
Lo studio di oggetti come buchi neri o i primi istanti di vita dell’universo dopo il Big Bang, in cui la teoria della relatività generale vacilla a causa della presenza della singolarità, porta gli scienziati a valutare condizioni estreme, non distanti dalla scala di Planck e in tali condizioni la descrizione in termini di dimensioni di Planck potrebbe essere l’unica realmente appropriata.

Per esempio, su scala atomica, considerando la massa di due protoni e le loro cariche elettriche, la forza gravitazionale che causa la loro attrazione reciproca e la forza elettrica che ne causa la repulsione sono molto diverse, con la gravità che è 10-36 volte più debole. Alla scala di Planck però, ipotizzando di avere particelle aventi la massa di Planck a distanza di Planck, il rapporto fra le due forze sarebbe circa 1. A questa scala potrebbe nascondersi la chiave per il prossimo salto nella comprensione delle leggi ultime dell’universo.

Oggi le unità di Planck sono largamente utilizzate in quanto permettono di semplificare le equazioni e concentrarsi sul loro profondo significato fisico. Per questo sorgono degli interrogativi che per ora possono trovare solo risposte attraverso pura speculazione. Come la questione se la lunghezza di Planck debba essere considerata un limite invalicabile alla possibilità di misurare una distanza o se essa debba essere considerata un “quanto” elementare di spazio per cui lo spazio possa incrementarsi solo di quantità discrete pari a multipli della lunghezza di Planck.

Il rovescio della medaglia è che trovare risposte o conferme a questi interrogativi tramite indagine sperimentale è, almeno per ora, pressoché impossibile, poiché per esaminare fenomeni che avvengono a quelle scale si richiedono energie altrettanto straordinarie. Basti pensare che gli acceleratori di particelle che sono usati oggi per indagare il comportamento della materia possono produrre energie nell’ordine di 1013eV. L’energia di Planck, calcolata a partire dalle sue unità fondamentali, è di circa 1,2 x1031eV.
Siamo ancora in difetto di un fattore 1018!

←

→

Pagine: 1 2 3 4 5